Maximum average of subtree values in a given Binary Tree

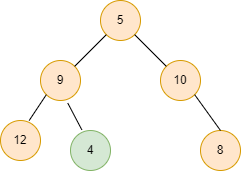
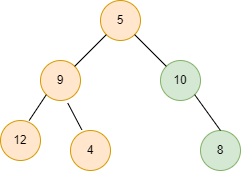
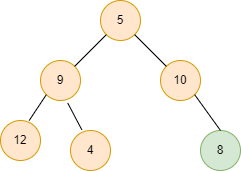
Approach

The idea is simple: we find the sum of all the nodes, count all the nodes for every subtree in the given binary tree, and calculate the average value (sum of all the nodes/count of nodes) for every subtree.

Sum of all the nodes in a subtree starting with a node = sum of all the nodes in the left subtree + sum of all the nodes in the right subtree + root node of the subtree.

Similarly, the count of nodes in a subtree = count of nodes in the left subtree + count of nodes in the right subtree + 1 (for the root node of the subtree).

For calculating the count and sum of nodes, we will use the concept of recursion. Finally, we take the maximum of all the calculated average values and return the maximum average of subtree values.

Algorithm:

Declare a global maxm_avg = -10000000 variable of double data type to store the required maximum average of subtree values because the average value can be a decimal number and the minimum subtree average can't be smaller than this value. 

In the main() function, call the maximum_avg_subtree() function, which calculates the maximum average value and passes the tree’s root node as an argument in it. For every test case, we will have to reset the value of maxm_avg to -10000000 so that the last test case's value is deleted.
 

Steps for maximum_avg_subtree() function:

• Declare a count variable and initialize it with 0.
• Call subtree_sum function and pass the root and count as an argument.
• Return the maxm_avg.

Steps for the subtree_sum() function:

• If root = NULL, the average value will be 0, so we return 0. It is the base case of our recursion.
• Create two variables, left_count = 0 and right_count = 0. It stores the count of the nodes in the left and right subtree, respectively.
• Create a left_sum variable that stores the sum of all the nodes in the left subtree, left_sum = subtree_sum(root->left, left_count).
• Similarly, create a right_sum variable that stores the sum of all the nodes in the right subtree, right_sum = subtree_sum(root->right, right_count).
• Calculate the sum of all the nodes of the subtree starting with any root, which is equal to the sum of all the nodes in the left subtree, right subtree and the value of the current root, sum = left_sum + right_sum + root->value.
• Similarly, calculate the count equal to the sum of the count of left subtree nodes, the count of right subtree nodes and 1 (for the current root node), count = left_count + right_count + 1.
• Now, calculate the maximum average seen so far, maxm_avg = max(maxm_avg, sum / count).
• Finally, return the sum.

Finally, print the maxm_avg, the maximum average of subtree values.

Code in C++

#include<bits/stdc++.h>
using namespace std;

struct Node {
    int val;
    Node *left;
    Node *right;
    Node(int x)
    {
        val = x;
        left = NULL;
        right = NULL;
    }
};

double maxm_avg = -10000000.0;

int subtree_sum(Node* root, int &count) {
    if (root == NULL)
        return 0;

    int left_count = 0;
    int right_count = 0;
    int left_sum = subtree_sum(root->left, left_count);
    int right_sum = subtree_sum(root->right, right_count);
    int sum = left_sum + right_sum + root->val;
    count = left_count + right_count + 1;
    maxm_avg = max(maxm_avg, (double)sum / count);
    return sum;
}
double maximum_avg_subtree(Node* root) {
	maxm_avg = -10000000.0;
    int count = 0;
    subtree_sum(root, count);
    return maxm_avg;
}

int main()
{
    Node* root = new Node(15);
    root->left = new Node(8);
    root->right = new Node (6);

    cout << maximum_avg_subtree(root) << endl;

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output

9.66667

You can also try this code with Online C++ Compiler

Run Code

Complexity Analysis

Time complexity: O(n), where n is the number of nodes in the given tree as we are traversing all the nodes.

Space complexity: O(h), where h is the height of the given binary tree.

Frequently Asked Questions

What is the purpose of a binary tree?

Binary trees are primarily used in computing for searching and sorting because they allow data to be stored hierarchically. Insertion, deletion, and traversal are some of the most common operations that can be performed on binary trees.

Is it possible for a binary tree to have only one child?

A binary tree is one in which no node has more than two children, and each child is either a left or right child, even if it is the parent's only child. A full binary tree is one with two children for each internal node.

What is the difference between a binary search tree and a binary tree?

A Binary Tree follows one simple rule: each parent node can have no more than two child nodes, whereas a Binary Search Tree is simply a variant of the binary tree that uses a relative order to organise the nodes in the tree.

How to recognize a leaf node in a binary tree?

Steps in C++:

• If root==NULL, return.
• If root->left==NULL and root->right==NULL, it is a leaf node, print the node data.
• Repeat the process for both the left and the right subtree.

Conclusion

This article discussed the average value of a subtree and the problem, the Maximum average of subtree values in a given Binary Tree with examples for better understanding and its C++ code.

Recommended Reading:

• Maximum Spiral Sum in Binary Trees
• Count the Number of Nodes
• Sum of Heights of all Individual Nodes of the Binary Tree
• Maximum Level Sum in N-ary Tree
• Top Tree Interview Questions

Do check out The Interview guide for Product Based Companies as well as some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, Uber, Microsoft, etc. on Coding Ninjas Studio.

Check out this problem - Root To Leaf Path

Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.

Thank you for reading!