Problem
Given an integer ‘N’ denoting the number of nodes in the graph, an array of pairs ‘arr’ of length ‘M’, denoting an edge and another array ‘queries’ of length ‘Q’, find the maximum element in the connected component of the node having a value equal to ‘queries[i]’ for every 1<=i<=Q.
In other words, we are given edges of a graph, and we are required to find the maximum element in the connected component of the given node.
Example -
Input: ‘arr’ = [ {1, 2}, {2, 4}, {3, 5} ] and ‘queries’ = [3, 2, 4].
Output: 5 4 4
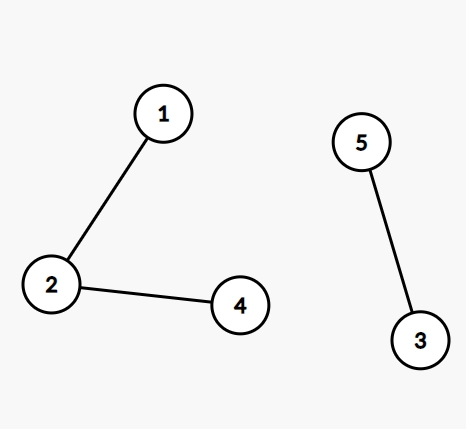
For the first query - ‘queries[0]’, the given node is 3. We can see that the connected component of 3 consists of only two nodes - 3 and 5. Since we need the maximum element in the connected component, so the answer for the first query is 5.
For the second query - ‘queries[1]’, the given node is 2. The connected component of 2 has three nodes - 1,2,4. So, the maximum element in the connected component of 2, and the answer for the second query is 4.
Similarly, for the third query - ‘queries[2]’, the given node is 4. The maximum element in the connected component of 4 is 4 itself.
Naive Approach
One simple approach to solving this problem is to do dfs/bfs for each query and keep track of the maximum element. To implement this, we can first create an adjacency list from the given edges. For every query, initialize ‘ans’ = 0. Then we can perform DFS Algorithm and update ‘ans’ as ‘ans’ = max(‘ans’, ‘node’) for every node we visit. After this, ‘ans’ will have a value equal to the maximum element in the connected component.
C++ Code
You can also try this code with Online C++ Compiler |
Output
5 4 4Time Complexity = O(N * Q)
For every query, we are performing DFS to get the maximum element of the connected component. In the worst case, the entire graph can be connected, so, a single DFS will have O(N) complexity. Therefore the total time complexity for Q queries is O(N * Q).
Space Complexity = O(N + M)
First, we are creating an adjacency list from the given edges. For M edges and N nodes, the adjacency list will have O(N + M) space complexity.
For every query, we are creating stack and visited array of length O(N). So the total space complexity of the approach is O(N + M).




