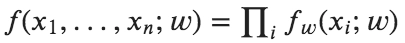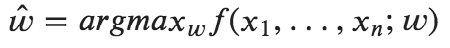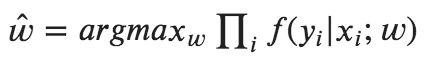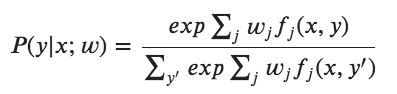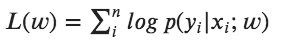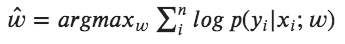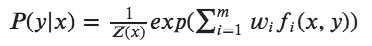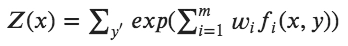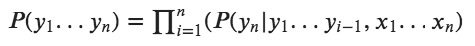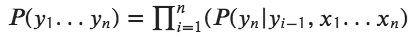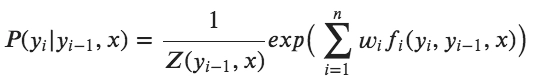Maximum Entropy Model

Log-Linear Model

The log-linear model uses a linear combination of features and weights to find the predicted label with maximum log-likelihood. The log-likelihood is the logarithm of the likelihood function. Since the logarithm function is a monotonic increasing function, maximizing the log-likelihood maximizes the likelihood.

We describe the probability as:

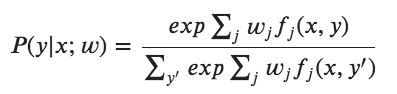
The function f(x,y) is a function that can account for relations between data and labels. It expresses some characteristics of the data point. It results in a value of 0 or 1 depending on the absence or presence. The wj is a weight of the feature function that captures how closely a given feature is related to a provided label. In the training process, wj is randomly initialized initially. The training process will learn the weight through gradient descent with some optimization methods. 

Approach

In the training phase, we have to find weight w. Let us start with the log-likelihood function:

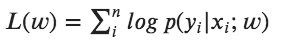
This function L(w) measures how well w explains the labeled data. The higher value of P(y|x; w) greater is the value of L(w). The maximum-likelihood function uses the argmax function to find the best values for the parameter w:

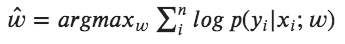
The process involves iterating through training data many iterations.

1. Initially, initialize the w to some random values.
2. Keep iterating through each input. During each iteration, we update the weight by finding the derivative of L(w) concerning wj. 
3. Updating vector was below and repeated until converged.

Maximum Entropy Likelihood

The maximum entropy model is log-linear. MaxEnt handles multinomial distribution. The maximum entropy principle states that we have to model the given set of data by finding the highest entropy to satisfy the constraints of our previous knowledge.

To find the probability for each class, Maximum Entropy is defined as:

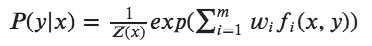
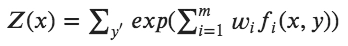
Applications

MaxEnt classification is a more classical machine learning task and solves problems beyond natural language processing. Here are a few:

• Sentiment analysis (e.g., given a product review, the reviewer likes and dislikes about the product).
• Preferences (e.g., Given a person's demographics, who will a person vote for? Would they prefer Superman, Batman, or the Teenage Mutant Ninja Turtles? etc.).
• Diagnosis (e.g., Given characteristics of several medical images and patient history, what medical condition is a person at risk of having?).

Maximum Entropy Markov Model

There are many systems where there is a time or state dependency. These systems evolve through a sequence of states, and past states influence the current state. For example, stock prices, DNA sequencing, human speech, or words in a sentence.

Maximum Entropy Markov Model makes use of state-time dependencies,i.e., it uses predictions of the past and the current observation to make the current prediction.

In image analysis, we're required to classify the object into one of many classes. We estimate the probability for each class. Rather than take a hard decision on one of the outcomes, it's better to output probabilities, which will benefit downstream tasks.

Multinomial logistic regression is also called softmax regression or Maximum Entropy (MaxEnt) classifier. Entropy's related to the disorder. Higher the disorder, less predictable the outcomes, and hence more information. For example, an unbiased coin has more information (and entropy) than one that mostly lands up heads. MaxEnt is about picking a probability distribution that maximizes the entropy.

Then, there's Markov Chain. It models a system as a set of states with probabilities assigned to state transitions. While MaxEnt computes probabilities for each input independently, the Markov chain recognizes a dependency from one state to the next. Thus, MEMM maximizes entropy plus using state dependencies (Markov Model).

The MEMM has dependencies between each state and the full observation sequence explicitly. MEMM has only one transition probability matrix. This matrix encapsulates previous states y(i−1) and current observation x(i) pairs in the training data to the current state y(i). Our goal is to find the P(y1,y2,…,yn|x1,x2,…xn). This is given by:

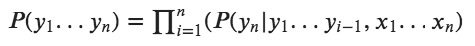
Since HMM only depends on the previous state, we can limit the condition of y(n) given y(n-1). This is the Markov independence assumption.

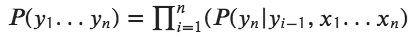
So MEMM defines using Log-linear model as:

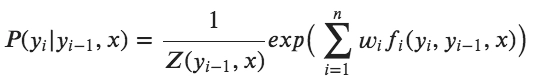
Shortcomings Of MEMM

MEMM suffers from what's called the label bias problem. Once we're in a state or label, the following observation will select one of many transitions leaving that state. However, the model as a whole would have many more transitions. If a state has only one outgoing change, the observation has no influence. Simply put, transition scores are normalized on a per-state basis.

Frequently Asked Questions

Q1. What is the condition for maximum entropy?

Ans. The principle of maximum entropy states that the probability distribution that best represents the current state of knowledge about a system is the one with the most significant entropy in the context of precisely stated primary data.

Q2. Is maximum entropy possible?

Ans. The maximum entropy principle (MaxEnt) states that the most appropriate distribution to model a given set of data is the one with the highest entropy among all those that satisfy our prior knowledge's constraints.

Q3. Which distribution has maximum entropy?

Ans. Therefore, the normal distribution is the maximum entropy distribution with a known mean and variance.

Key Takeaways

Let us brief the article.

Firstly, we saw the meaning of the maximum entropy model. Moving on, we saw the building blocks of the maximum entropy model like maximum likelihood and log-linear model. Later, we saw the approach used by the maximum entropy model. Later we saw the applications of the maximum entropy model. Lastly, we saw the model of maximum entropy likelihood,i.e., maximum entropy Markov model, and some of its shortcomings. That's the end of the article.

I hope you all like it.

Happy Learning Ninajs!