Introduction
We are given an array of ‘N’ integers. We need to construct two Binary Search Trees starting from both the left and right ends, and then return the maximum height of the Binary Search Tree among both of them.
Also see, Data Structures
Let us see a few examples:-
Input: [3, 1, 5, 2, 4]
Output: 2
Explanation: The following two trees will be formed from both the left and right ends.
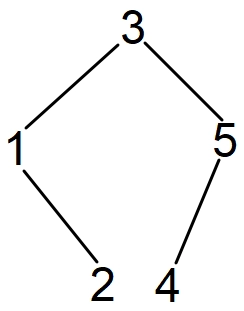
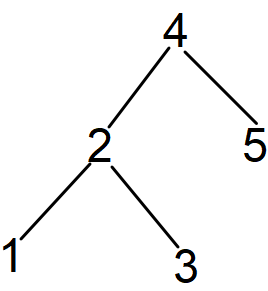
Both the Binary Search Trees have a height of 2. Hence, the maximum height is 2.
Approach
We will first implement a class for Tree. We will implement the Insert function so that we can add a node to the Binary Search Tree.
Using our tree class, we will construct both the Binary Search Trees from the left and right end and then find the height of both the trees and then return the maximum among them.
Refer to the below implementation of the above approach.
static class node
{
int key;
node left, right;
};
// Function to create a node of a tree.
static node newNode(int item)
{
node temp = new node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
/*
Function to insert a node to a tree
*/
static node insert(node node, int key)
{
/*
If the tree is empty,
return a new node
*/
if (node == null)
return newNode(key);
/* Otherwise, recur down the tree */
if (key < node.key)
node.left = insert(node.left, key);
else if (key > node.key)
node.right = insert(node.right, key);
/* return the (unchanged) node pointer */
return node;
}
/*
Function to Find
the maximum depth
of a tree.
*/
static int maxDepth(node node)
{
if (node == null)
return 0;
else
{
/* compute the depth of each subtree */
int lDepth = maxDepth(node.left);
int rDepth = maxDepth(node.right);
/* use the larger one */
if (lDepth > rDepth)
return (lDepth + 1);
else
return (rDepth + 1);
}
}
static int maxHeight(int a[], int n)
{
/*
Creating the tree
from the left end
of the array.
*/
node rootA = null;
rootA = insert(rootA, a[0]);
for (int i = 1; i < n; i++)
rootA = insert(rootA, a[i]);
/*
Creating the another
tree from the right
end of the array.
*/
node rootB = null;
rootB = insert(rootB, a[n - 1]);
for (int i = n - 2; i >= 0; i--)
rootB =insert(rootB, a[i]);
// Finding the heights of both the trees
int HeightOfA = maxDepth(rootA) - 1;
int HeightOfB = maxDepth(rootB) - 1;
return Math.max(HeightOfA, HeightOfB);
}
Time Complexity: The time complexity for the above approach is O(N), (where ‘N’ is the total number of nodes in the tree) because we are just constructing a tree that takes O(N) time and finding the depth of the tree also takes O(N) time.
Space Complexity: The space complexity for the above code is O(N) because we are constructing two trees of ‘N’ nodes.
Check out this problem - Root To Leaf Path




