Approach
To fully understand the approach used to solve this problem. One needs to know about the Ford-Fulkerson method. The ford-Fulkerson method is a greedy algorithm that computes the maximum flow in a flow network.
Have a look at the article mentioned below to know more about ford-Fulkerson method.
Ford-Fulkerson Algorithm for Maximum Flow
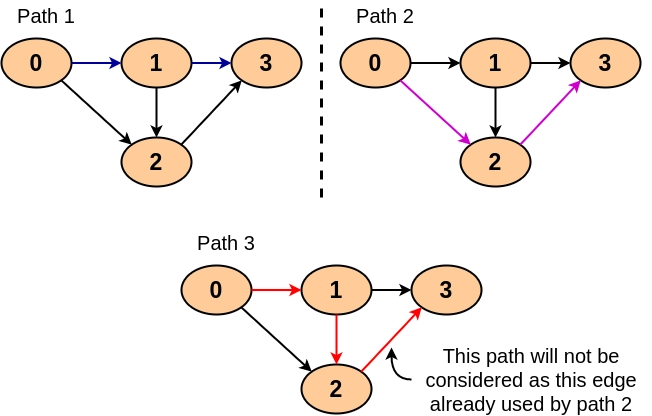
The basic idea behind the approach is that if there exists a path between the source and destination vertex we find that path and add it to the total paths. Then we find another path and this process continues until all of the paths are not explored.
The idea behind the ford-Fulkerson algorithm:
-
Start with initial available paths as 0.
-
While there is an augmenting path from source to destination.
-
Add this path to the total available paths.
-
Return total available paths.
This problem can be solved using the approach used in the maximum flow problem in which we use the ford-Fulkerson algorithm. To know more about the ford-fulkerson algorithm you can have a look at the article mentioned below:
Maximum Flow 🥳
Pseudocode
Get_Paths (Graph, src, dest):
int parent[total number of vertices] <- {0, 0,....., 0}
int total_paths = 0;
while (there exists a path between src and dest):
int path <- 0;
int v <- dest;
while v != src:
int u = parent[v];
path = Graph[u][v];
Graph[u][v] = 0;
END_WHILE
total_paths = total_paths + path;
END_WHILE
return total_paths;
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
// function to check whether there exists a path between a source and destination
// vertex
bool pathExits(vector<vector<int>> graph, int src, int dest, vector<int> &parent){
// bool array to keep track of visited vertices
vector<bool> visited(graph.size(), false);
// queue for bfs
queue<int> q;
// pushing source vertex into our queue
q.push(src);
// marking source vertex as visited
visited[src] = true;
parent[src] = -1;
// bfs
while(!q.empty()){
int u = q.front();
q.pop();
for(int v = 0; v < graph.size(); v++){
// if there exist an edge between u and v
// and it's still not visited push it into the queue
if(!visited[v] && graph[u][v] == 1){
q.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
// return true if we have visited the destination
// vertex, else it will return false;
return visited[dest];
}
int getPaths(vector<vector<int>> graph, int src, int dest){
vector<int> parent(graph.size());
int total_paths = 0;
while(pathExits(graph, src, dest, parent)){
int path = 0;
for(int v = dest; v != src; v = parent[v]){
// getting parent vertex
int u = parent[v];
// if there's an edge between u and v
// path will become 1
path = graph[u][v];
// removing the edge as we need edge disjoint paths
graph[u][v] = 0;
}
total_paths += path;
}
return total_paths;
}
int main(){
vector<vector<int>> graph = {
{0, 1, 1, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
};
int src = 0;
int dest = 7;
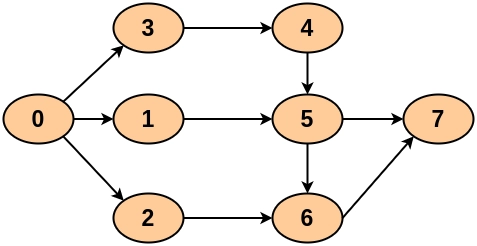
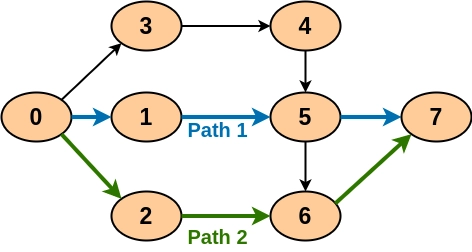
cout << "Maximum number of edge disjoint paths between " << src << " and " << dest << ": " << getPaths(graph, src, dest) << endl;
return 0;
}

You can also try this code with Online C++ Compiler
Output
Maximum number of edge disjoint paths between 0 and 7: 2
Time Complexity
The time complexity of the above program is O(EV^3), where E is the number of edges in our graph and V is the number of vertices. As we are using bfs to check whether the path exists between the source and destination vertex again and again that is why the time complexity of our program is O(EV^3).
Space Complexity
To implement a bfs we need to use a queue. So, the space complexity of our program is O(V), where V is the number of vertices in our program.
Frequently Asked Questions
What are graphs?
One common type of data structure is a graph, which consists of a finite number of nodes (also called vertices) and a finite number of connected edges. An edge is a pair (u, v) that denotes a connection between u and v vertices.
What are cyclic and acyclic graphs?
If a network has a cycle—a continuous set of nodes without any repeating nodes or edges that connects back to itself—then it is said to be cyclic. Acyclic graphs are those without cycles.
What are directed and undirected graphs?
Edges in directed graphs point from one end of the graph to the other. The edges in undirected networks merely link the nodes at each end.
Conclusion
In this article, we have extensively discussed a problem related to graph theory in which we have to print the maximum number of edge-disjoint paths between two vertices. We have seen an implementation in which we are using the Ford-Fulkerson algorithm.
Recommended Problems:
If you think this blog has helped you enhance your knowledge about the above question, and if you would like to learn more, check out our articles
and many more on our website.
Visit our website to read more such blogs. Make sure that you enroll in the courses provided by us, take mock tests and solve problems and interview puzzles available. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations.
Please upvote our blog to help other ninjas grow.
Happy Learning!