Maximum Product of Two Non-intersecting Paths in a Tree

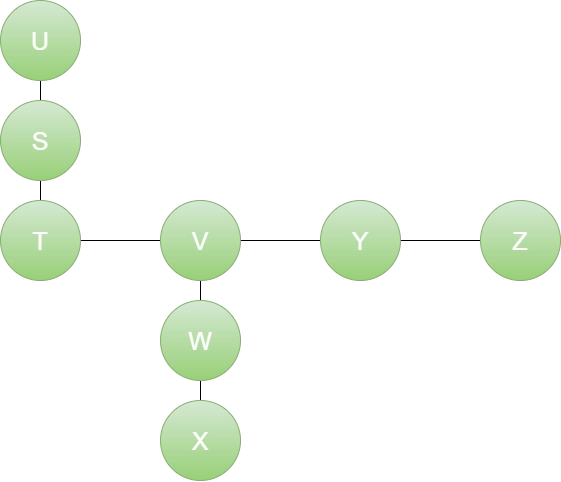
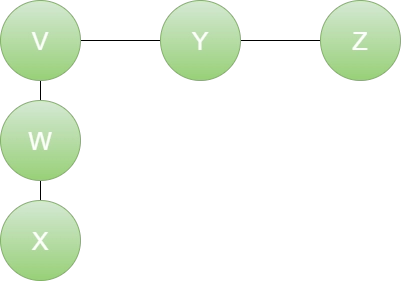
Approach

This issue can be resolved by using DFS Algorithm to navigate the tree. Find the pathways that will remain distinct if the connecting edge is eliminated. The path should then be iterated on to determine its length. The product of lengths of the pathways will then be determined by pairing them. The Two are taken into account such that their combined output is at its maximum. The algorithm will be something like this:

• Iteration over the edges,
   
• For every edge, remove it,
   
• Then, we will find the length of the path in both connected components, and 
   
• Multiply the lengths of these paths.
   

A modified depth-first search can determine the length of a path in a tree by calling for the maximum path at each neighbor and adding the two maximum lengths returned, which will be the maximum path length at the subtree rooted at the present node.

Algorithm

1. We will create a list that will contain the edges.
    
2. We will use the “addEdge” method to add the edges to the graph.
    
3. Then, we will call the “maxProductOfTwoPath” method by giving the graph and its size as the arguments.
   
   1. Here, we will first remove all the edges one by one.
       
   2. Then we will call the “dfs” method to find the lengths of the first and second maximum in the subtrees.
       
   3. We will store the values returned by dfs in “path_1” and “path_2”.
       
   4. Then we will call the “max” method to find the maximum product.
       
4. After the function has successfully returned the maximum product, we will print the output.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

int dfs(vector<int> graph[], int& currMax, int a, int v) {
    
	/*  Function to find the lengths of the first and second maximum in the subtrees. 
	    currMax is to store the overall maximum. */
	
	int max_1 = 0, max_2 = 0, total = 0;

	/* A loop through all the neighbors of a. */
	for (int i = 0; i < graph[a].size(); i++)
	{
		/* If neighbor is v, then we will skip it. */
		if (graph[a][i] == v)
			continue;

		/* We will call it recursively with the current neighbor as the root. */
		total = max(total, dfs(graph, currMax, graph[a][i], a));

		// This will get max from one side and then update the values.
		if (currMax > max_1)
		{
			max_2 = max_1;
			max_1 = currMax;
		}
		else
			max_2 = max(max_2, currMax);
	}

	/* We will store total length by adding the values of max and second max. */
	total = max(total, max_1 + max_2);

	currMax = max_1 + 1;
	return total;
}

/* This method will return the maximum product of the length of two non-intersecting paths. */
int maxProductOfTwoPath(vector<int> graph[], int size)
{
	int res = INT_MIN;
	int path_1, path_2;

	/* We will remove all the edges one by one and call the dfs on both the subtrees. */
	for (int i = 1; i < size+2; i++)
	{
		for (int j = 0; j < graph[i].size(); j++)
		{

			int currMax = 0;
			path_1 = dfs(graph, currMax, graph[i][j], i);

			currMax = 0;
			path_2 = dfs(graph, currMax, i, graph[i][j]);

			res = max(res, path_1 * path_2);
		}
	}
	return res;
}

void addEdge(vector<int> graph[], int u, int v)
{
	graph[u].push_back(v);
	graph[v].push_back(u);
}

int main()
{
	int edges[][2] = {{1, 2}, {2, 4}, {3, 1}, {5, 4}, {7, 8}, {8, 4}, {5, 6} };
	int size = sizeof(edges)/sizeof(edges[0]);

	/* There are size edges, so +1 for nodes and +1 for 1-based indexing */
	vector<int> graph[size + 2];
	for (int i = 0; i < size; i++)
		addEdge(graph, edges[i][0], edges[i][1]);
	
	cout << "The maximum product of two non-intersecting paths in a tree: " << endl;
	cout << maxProductOfTwoPath(graph, size) << endl;
	return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output

Implementation in Java

import java.util.*;

class CodingNinjas{
    static int currMax;
    
    /* It returns the maximum length path in the subtree rooted at a after removing the edge connecting a and v. */
    static int dfs(Vector<Integer> graph[], int a, int v)
    {
    	
    	/* This will find the lengths of first and second maximum in subtrees.
    	    currMax is to store the overall maximum. */
    	int max_1 = 0, max_2 = 0, total = 0;
    
    	// We will loop through all the neighbors of a.
    	for(int i = 0; i<graph[a].size(); i++)
    	{
    		
    		// If the neighbor is v, then we will skip it.
    		if (graph[a].get(i) == v)
    			continue;
    
    		// We will call recursively with the current neighbor as the root.
    		total = Math.max(total, dfs(
    			graph, graph[a].get(i), a));
    
    		// Get max from one side and update the values.
    		if (currMax > max_1)
    		{
    			max_2 = max_1;
    			max_1 = currMax;
    		}
    		else
    			max_2 = Math.max(max_2, currMax);
    	}
    
    	// We will store total length by adding max and second max.
    	total = Math.max(total, max_1 + max_2);
    
    	currMax = max_1 + 1;
    	return total;
    }
    
    // Method will return the maximum product of the length of the two non-intersecting paths.
    static int maxProductOfTwoPath(Vector<Integer> graph[], int size)
    {
    	int res = Integer.MIN_VALUE;
    	int path_1, path_2;
    
    	/* One by one removing all edges and
    	   calling dfs on both subtrees. */
    	for(int i = 1; i < size + 2; i++)
    	{
    		for(int j = 0; j < graph[i].size(); j++)
    		{
    			
    			// Calling dfs on subtree rooted at
    			// graph[i][j], excluding edge from graph[i][j]
    			// to i.
    			currMax = 0;
    			path_1 = dfs(graph, graph[i].get(j), i);
    
    			// Calling dfs on subtree rooted at
    			// i, edge from i to graph[i][j]
    			currMax = 0;
    			path_2 = dfs(graph,i, graph[i].get(j));
    
    			res = Math.max(res, path_1 * path_2);
    		}
    	}
    	return res;
    }
    
    static void addEdge(Vector<Integer> graph[], int a, int v)
    {
    	graph[a].add(v);
    	graph[v].add(a);
    }
    
    public static void main(String[] args)
    {
    	int edges[][] = {{1, 2}, {2, 4}, {3, 1}, {5, 4}, {7, 8}, {8, 4}, {5, 6} };
    					
    	int size = edges.length;
    
    	// There are size edges, so +1 for nodes
    	// and +1 for 1-based indexing
    	@SuppressWarnings("unchecked")
    	Vector<Integer> []graph = new Vector[size + 2];
    	for(int j = 0; j < graph.length; j++)
    		graph[j] = new Vector<Integer>();
    		
    	for(int i = 0; i < size; i++)
    		addEdge(graph, edges[i][0], edges[i][1]);
        
        System.out.print("The maximum product of the two non-intersecting paths in a tree is: ");
    	System.out.print(maxProductOfTwoPath(graph, size) + "\n");
    }
}

You can also try this code with Online Java Compiler

Run Code

Output

Implementation in Python

def dfs(graph, currMax, u, v):
	
	# Method to find lengths of first and second maximum in the subtrees. 
	# currMax is to store the overall maximum.
	max_1 = 0
	max_2 = 0
	total = 0

	# We will loop through all the neighbors of u.
	for i in range(len(graph[u])):
		
		# If the neighbor is v, then skip it.
		if (graph[u][i] == v):
			continue

		# Call recursively with the current neighbor as the root.
		total = max(total, dfs(graph, currMax, graph[u][i], u))

		# Get max from one side and update the values.
		if (currMax[0] > max_1):
			max_2 = max_1
			max_1 = currMax[0]
		else:
			max_2 = max(max_2, currMax[0])

	# Store the total length by adding max and second max.
	total = max(total, max_1 + max_2)

	currMax[0] = max_1 + 1
	return total

# Method will return the maximum product of the length of two non-intersecting paths.
def maxProductOfTwoPath(graph, N):
	res = -999999999999
	path_1, path_2 = None, None

	# We will remove all the edges and call dfs on both the subtrees.
	for i in range(N):
		for j in range(len(graph[i])):
			
			# Calling the dfs on subtree rooted at graph[i][j], excluding edge from graph[i][j] to i.
			currMax = [0]
			path_1 = dfs(graph, currMax, graph[i][j], i)

			# Calling the dfs on subtree rooted at i, edge from i to graph[i][j].
			currMax = [0]
			path_2 = dfs(graph, currMax, i, graph[i][j])

			res = max(res, path_1 * path_2)
	return res

def addEdge(graph, u, v):
	graph[u].append(v)
	graph[v].append(u)


if __name__ == '__main__':
	edges = [[1, 2], [2, 4], [3, 1], [5, 4], [7, 8], [8, 4], [5, 6]]
	N = len(edges)

	graph = [[] for i in range(N + 2)]
	for i in range(N):
		addEdge(graph, edges[i][0], edges[i][1])
		
	print("The maximum product of two non-intersecting paths in a tree is: ")
	print(maxProductOfTwoPath(graph, N))

You can also try this code with Online Python Compiler

Run Code

Output

Complexity Analysis 

Time Complexity

Since we are using Nested Loops.

Thus the time complexity is O(N²), where N is the Size.

Space Complexity

O(N), where 'N' is the size.

Since we are using an array, which will take O(N) space.

Frequently Asked Questions

What is BST used for?

A binary search tree (BST) is a data structure that provides a quick method for iterating through the items in sorted order while also enabling quick insertion, removal, and lookup of things.

What is an internal node?

An internal node is a node in a tree that has one or more child nodes or, alternatively, a node that is not a leaf. We can also call it a nonterminal node.

How many paths are in a graph if it has two vertices?

A path is like a route between any two vertices of the graph. If a graph has only two nodes X and Y, there are two paths with one vertex, X and Y, and two paths XY and YX with two vertices.

Does sizeof work on arrays?

Only fixed-size arrays can be used with sizeof() (which can be static, stack-based, or in a struct). You will always obtain the size of a pointer if you apply it to an array made with malloc (or new in C++).

Differentiate between an internal and external node in a binary tree?

A node that is internal has at least one child branch, whereas a node that is external has none.

Conclusion

In this article, we have studied how to write a program to find the maximum product of two non-intersecting paths in a tree. We hope that this article has provided you with the help to enhance your knowledge regarding hashmap and if you would like to learn more, check out our articles on Advantages of bst over hash table, Reverse a path in bst using queue, and Minimum distance between bst nodes.

Recommended Problems:

• Unique Paths
• Longest Path Directed Acyclic Graph
• Longest Path In A Tree
   

Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. Enroll in our courses and refer to the mock test and problems available. Take a look at the interview experiences and interview bundle for placement preparations.

Merry Learning!