Brute Force
Now the brute force approach for this problem is very simple. We will calculate all possible answers, i.e., path sum from every leaf to every other leaf, and then return the maximum path sum among them. But this method will cost us a lot of time and, time is money in coding, so let’s now see the efficient approach for the problem.
Intuition
The way we are thinking about solving this problem is that we will calculate the maximum path sum leaf to leaf in constant time. Our idea here is to start from the bottom of the tree and then return each node's maximum sum node-to-leaf path to its parent node. We calculate the maximum sum path rooted at each node and update the max sum during the traversal.
It will become more clear once we discuss the algorithm.
Algorithm
We will declare the following functions.
- 'findMaxSumPath()': This will return our final answer. In this function, we will declare a variable 'MAX_SUM_PATH' and will initialize it to -1. This variable will store the final answer, i.e., the maximum path sum from leaf to leaf. Inside this function, we will call the function' findMaxSumPathHelper()', which will take two parameters i,e, tree's root and the variable 'maxPathSum' by reference.
2. 'findMaxSumPathHelper()': This is where all the magic is going to happen. It is going to be a recursive function that will accept two parameters:
- 'ROOT' is the root of our tree.
- 'MAX_PATH_SUM' is our final answer.
Recursive Case :
- We will make two calls to this function, i.e., left and right subtree of the 'ROOT' node, and store their answers in the variables 'MAX_SUM_LEFT_PATH' (maximum sum along the path starting from the current node('ROOT') and ending at a leaf node in the left subtree) and the 'MAX_SUM_RIGHT_PATH' (maximum sum along the path starting from the current node('ROOT') and ending at a leaf node in the right subtree) respectively.
- Then we will update the value of 'MAXPATHSUM' as:
'MAX_PATH_SUM' = max('MAX_PATH_SUM' , 'MAX_SUM_LEFT_PATH' + ' MAX_SUM_RIGHT_PATH' + 'ROOT'->val)
3. Then we will return the maximum sum in the subtree starting from the current node(root) to leaf i.e. max(‘MAX_SUM_LEFT_PATH', ‘MAX_SUM_RIGHT_PATH’') + ‘ROOT’->val
Below is the implementation of the function.
Code
#include <iostream>
#include <queue>
using namespace std;
// Binary Tree Node Class.
template <typename T>
class BinaryTreeNode
{
public:
T val;
BinaryTreeNode<T> *left;
BinaryTreeNode<T> *right;
BinaryTreeNode(T val)
{
this->val = val;
left = NULL;
right = NULL;
}
};
long long int findMaxSumPathHelper(BinaryTreeNode<int> *root, long long int &maxPathSum)
{
if (root == NULL)
{
return -1;
}
if (root->left == NULL && root->right == NULL)
{
return root->val;
}
// Variable to store the maximum sum of the path from the current node to leaf in the left subtree.
long long int maxSumLeftPath = findMaxSumPathHelper(root->left, maxPathSum);
// Variable to store the maximum sum of the path from the current node to leaf in the right subtree.
long long int maxSumRightPath = findMaxSumPathHelper(root->right, maxPathSum);
// If the current node has both children, update the value of maxPathSum.
if (root->left != NULL && root->right != NULL)
{
maxPathSum = max(maxPathSum, maxSumLeftPath + maxSumRightPath + root->val);
return max(maxSumLeftPath, maxSumRightPath) + root->val;
}
else if (root->left == NULL)
{
return maxSumRightPath + root->val;
}
else
{
return maxSumLeftPath + root->val;
}
}
long long int findMaxSumPath(BinaryTreeNode<int> *root)
{
// Variable to store the maximum sum of the path between two leaves for the given tree.
long long int maxPathSum = -1;
// Calling 'findMaxSumPathHelper()' function to calculate 'MAX_PATH_SUM'.
findMaxSumPathHelper(root, maxPathSum);
return maxPathSum;
}
// Function to take user input.
BinaryTreeNode<int> *takeInput()
{
int rootData;
cin >> rootData;
if (rootData == -1)
{
return NULL;
}
BinaryTreeNode<int> *root = new BinaryTreeNode<int>(rootData);
queue<BinaryTreeNode<int> *> q;
q.push(root);
while (!q.empty())
{
BinaryTreeNode<int> *currentNode = q.front();
q.pop();
int leftChild, rightChild;
cin >> leftChild;
if (leftChild != -1)
{
BinaryTreeNode<int> *leftNode = new BinaryTreeNode<int>(leftChild);
currentNode->left = leftNode;
q.push(leftNode);
}
cin >> rightChild;
if (rightChild != -1)
{
BinaryTreeNode<int> *rightNode = new BinaryTreeNode<int>(rightChild);
currentNode->right = rightNode;
q.push(rightNode);
}
}
return root;
}
int main()
{
BinaryTreeNode<int> *root = takeInput();
cout << findMaxSumPath(root) << endl;
}

You can also try this code with Online C++ Compiler
Input
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
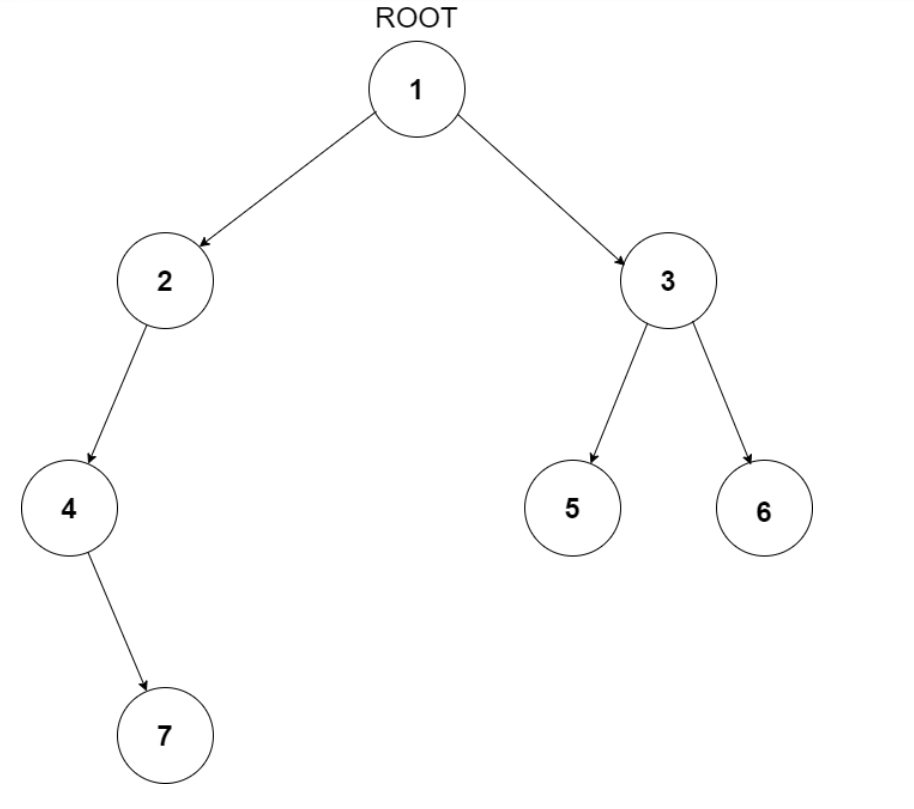
The input tree would look something like this.
Output
23
Time Complexity
O(N), where ‘N’ is the number of nodes in the tree.
Since we are traversing the entire tree only once so in total, we will be traversing every node once. Thus the time complexity is O(N).
Space Complexity
O(N), where 'N' is the number of nodes in the tree.
The recursive stack will take O(H) space where ‘H’ is the height of the tree. In the worst case, H will equal ‘N’ when each node in the tree has only one child(skewed tree). Thus, the space complexity is O(N).
Bonus
Now we can extend the above code to find to maximum path sum between any two nodes, Intuition behind this is very similar to the one we discussed above, so without wasting any time, let's have a look at the algorithm.
- Our answer will be stored in the variable 'MAX_SUM', which will store the maximum path sum out of all paths. We will initialize it to INT_MIN.
-
We will now create a helper function 'currentPathSum()', that will take two parameters, 'CURRENT_PEAK,' (root node) and 'MAX_SUM', and will return the maximum sum path from 'CURRENT_PEAK' and its descending nodes. Let us look at the functioning of this function:
- If our root node or 'CURRENT_PEAK' is NULL, we will return 0 as this is the maximum sum possible from a NULL Node.
- We will make two calls to this function for the left and right child of 'CURRENT_PEAK' and store the answer in 'MAX_PATH_SUM_LEFT' and 'MAX_PATH_SUM_RIGHT,' respectively.
- Now we will create a new variable 'CURRENT_SUM' and initialsie it as ('MAX_PATH_SUM_LEFT' + 'MAX_PATH_SUM_RIGHT' + (CURRENT_PEAK->data)).
- 'MAX_SUM' will be updated as the maximum of 'MAX_SUM' and 'CURRENT_PATH_SUM'.
- Then we will return the sum of 'CURRENT_PEAK_NODE' and the maximum among 'MAX_PATH_SUM_LEFT' and 'MAX_PATH_SUM_RIGHT'. This will be used for calculating the maximum sum path value for the parent nodes.
- Return the answer, i.e., ‘MAX_SUM’.
Below is the implementation of the above algorithm.
Code
#include <iostream>
#include <queue>
#include<algorithm>
#include<climits>
using namespace std;
// Binary Tree Node Class.
template <typename T>
class BinaryTreeNode {
public:
T data;
BinaryTreeNode<T>* left;
BinaryTreeNode<T>* right;
BinaryTreeNode(T data) {
this->data = data;
left = NULL;
right = NULL;
}
};
int currentPathSum(BinaryTreeNode<int> *currentPeak, int &maxSum)
{
// Checking if the current node is NULL.
if (currentPeak == NULL)
{
return 0;
}
int maxPathSumLeft = max(currentPathSum(currentPeak->left,
maxSum), 0);
int maxPathSumRight = max(currentPathSum(currentPeak->right,
maxSum), 0);
int currentSum = maxPathSumLeft + maxPathSumRight +
(currentPeak->data);
// Updating the overall maximum sum.
maxSum = max(currentSum, maxSum);
return max(maxPathSumLeft, maxPathSumRight) +
(currentPeak->data);
}
int maxPathSum(BinaryTreeNode<int> *root)
{
int maxSum = INT_MIN;
// Calling the recursive function.
currentPathSum(root, maxSum);
// Returning the updated value.
return maxSum;
}
BinaryTreeNode<int>* takeInput() {
int rootData;
cin >> rootData;
if (rootData == -1) {
return NULL;
}
BinaryTreeNode<int>* root = new BinaryTreeNode<int>(rootData);
queue<BinaryTreeNode<int>*> q;
q.push(root);
while (!q.empty()) {
BinaryTreeNode<int>* currentNode = q.front();
q.pop();
int leftChild, rightChild;
cin >> leftChild;
if (leftChild != -1) {
BinaryTreeNode<int>* leftNode = new
BinaryTreeNode<int>(leftChild);
currentNode->left = leftNode;
q.push(leftNode);
}
cin >> rightChild;
if (rightChild != -1) {
BinaryTreeNode<int>* rightNode = new
BinaryTreeNode<int>(rightChild);
currentNode->right = rightNode;
q.push(rightNode);
}
}
return root;
}
int main() {
BinaryTreeNode<int>* root = takeInput();
cout<<maxPathSum(root);
}

You can also try this code with Online C++ Compiler
Input
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1

The input tree would look something like this
Output
23
Time Complexity
O(N), where ‘N’ is the number of nodes in the tree.
Since we are traversing the entire tree only once, the overall time complexity is O(N).
Space Complexity
O(N), where 'N' is the number of nodes in the tree.
The recursive stack will take O(H) space where ‘H’ is the height of the tree. In the worst case, H will equal ‘N’ when each node in the tree has only one child. Thus, the space complexity is O(N).
Check out this problem - Root To Leaf Path
Key Takeaways
Now you have understood how to find the maximum sum path from the leaf to leaf as well as the maximum path sum from any node to any node in the binary tree. Your adrenaline would be on the next level, But don't worry, we have a solution for that too. Head over to our practice platform Coding Ninjas Studio to practice top problems and many more. Till then, Happy Coding!





