McCulloch Pitt's Model of Neuron

Introduction  

Many people mistake Perceptron to be the first Artificial Neural Network. However, to clear any misconceptions, Perceptron is the most fundamental unit of the modern-day ANN. Not the first Artificial Neural Network. The McCulloch Pitt's Model of Neuron is the earliest logical simulation of a biological neuron, developed by Warren McCulloch and Warren Pitts in 1943 and hence, the name McCulloch Pitt’s model. As simplistic as it may seem, we have to take into consideration that it was built several decades ago. In this blog, we are going to understand the origin of modern-day Artificial Neural Networks. 

Also read about, Artificial Intelligence in Education

Model Architecture

The motivation behind the McCulloh Pitt’s Model is a biological neuron. A biological neuron takes an input signal from the dendrites and after processing it passes onto other connected neurons as the output if the signal is received positively, through axons and synapses. This is the basic working of a biological neuron which is interpreted and mimicked using the McCulloh Pitt’s Model.

Source - link

McCulloch Pitt’s model of neuron is a fairly simple model which consists of some (n) binary inputs with some weight associated with each one of them. An input is known as ‘inhibitory input’ if the weight associated with the input is of negative magnitude and is known as ‘excitatory input’ if the weight associated with the input is of positive magnitude. As the inputs are binary, they can take either of the 2 values, 0 or 1. 

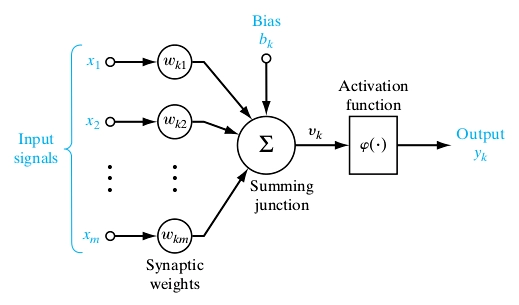
Source - link

Then we have a summation junction that aggregates all the weighted inputs and then passes the result to the activation function. The activation function is a threshold function that gives out 1 as the output if the sum of the weighted inputs is equal to or above the threshold value and 0 otherwise. 

So let’s say we have n inputs = { X1, X2, X3, …. , Xn }

And we have n weights for each= {W1, W2, W3, …., W4}

So the summation of weighted inputs X.W = X1.W1 + X2.W2 + X3.W3 +....+ Xn.Wn

If X ≥ ø(threshold value)

     Output = 1

Else

       Output = 0

Let’s Take a real-world example:

A bank wants to decide if it can sanction a loan or not. There are 2 parameters to decide- Salary and Credit Score. So there can be 4 scenarios to assess-

1. High Salary and Good Credit Score
2. High Salary and Bad Credit Score
3. Low Salary and Good Credit Score
4. Low Salary and Bad Credit Score

Let X1 = 1 denote high salary and X1 = 0 denote Low salary and X2 = 1 denote good credit score and X2 = 0 denote bad credit score

Let the threshold value be 2. The truth table is as follows

The truth table shows when the loan should be approved considering all the varying scenarios. In this case, the loan is approved only if the salary is high and the credit score is good. The McCulloch Pitt's model of neuron was mankind’s first attempt at mimicking the human brain. And it was a fairly simple one too. It’s no surprise it had many limitations-

1. The model failed to capture and compute cases of non-binary inputs. It was limited by its ability to compute every case with 0 and 1 only. 
2. The threshold had to be decided beforehand and needed manual computation instead of the model deciding itself.
3. Linearly separable functions couldn’t be computed.