Memoization in Javascript

Importance of Memoization

It is a performance-boosting approach that involves storing the results of function calls. It saves past findings and then retrieves them as needed throughout your programme. This improves CPU performance while reducing execution time.

A pure function should be a memoised function. This signifies that the execution of the function does not change. It should always return the same value when called with specific input, regardless of how many times the function is invoked.

Why not memorise the outcome of a function that performs not once, not twice, but multiple times? You'll just have to run this function once this way. This improves the performance of your software.

When to Employ Memoization in JavaScript

When a function is entirely pure and invoked, a pure function always returns the same value. When a function is impure, it gives different results every time it is called. Return values may be surprising if such values are cached.

When a programme performs an expensive computation, caching the results improves the program's speed. When employing memoization, the function doesn't have to recalculate its values, and it always returns the same results.

When API(Application Programming Interface ) calls are made from afar, use memoization in Javascript to avoid making several calls to the server when performing a repeating API call. You already know the outcome from the previous call, so you don't need to make another one to achieve the same results.

Recursive functions are functions that repeat themselves with recurring input values.

The Process of Memoization

Let's look at a real-life scenario. Assume you're reading a book with a warm, stylish, and appealing cover. A stranger approaches and inquires about the book's title and author. You'll probably turn the page, see the title and author's name, and respond to that stranger.

The book is appealing, and more people will be interested in learning more about it. If another person approaches you and inquires, you will not glance at the book's author and title again. You'll have to search for that information again if you don't recall. You may remember the details of the book at this time.

If a third party inquires about the book's details, you will have to rely on your recollection. Even if a hundred individuals ask about the book, the details will remain unchanged.

The concept of memoization is the same way. Memoisation saves the function results before returning them to the function caller when a function is invoked. Memoisation will return the result saved (cached) in memory when another caller points to the results of this function, and the function will not be called again. By caching the outcomes depending on their inputs, memorising avoids duplicate function calls.

Two major sub-concepts support the idea of memoization:

• Closure: Closure is a function that has been wrapped around (enclosed) with references to the relevant state (the lexical environment). In another way, Closure allows you to access the outer function's domain from the inside function. Closures are formed when a function is created in JavaScript.
• High-order function: A high-order function takes another function as an argument and returns another function as its output.

Memoization in JavaScript to Cache Function Values

Let's look at some instances to see how the concept of memoization in JavaScript might be used.

This is an example of a function that accepts an integer as an input and returns the square of that number.

const mysquare = num =>{
  let result = 0;
  for (let i = 1; i <= num; i++) {
    for (let j = 1; j <= num; j++) {
      result ++;
    }
  }
  return result;
}
console.log(mysquare(5));
console.log(mysquare(12));
console.log(mysquare(13));
console.log(mysquare(19));
console.log(mysquare(22));

 

You'll see that anytime you call the function, it will re-execute it and then return a squared value.

The implementation is simple and quick. The math is easy to understand. The main issue arises when you need to execute complex (expensive) calculations.

const mysquare = num =>{
  let result = 0;
  for (let i = 1; i <= num; i++) {
    for (let j = 1; j <= num; j++) {
      result ++;
    }
  }
  return result;
}
console.log(mysquare(191));
console.log(mysquare(899));
console.log(mysquare(5000));
console.log(mysquare(6467));
console.log(mysquare(7666));

 

This is ineffective. Instead, we may use the memoization concept to remember the outcome of mysquare() when it was initially called. The software will not have to perform this function again if we call it with the same input.

Let's implementt the memoization in JavaScript program. To do this, the program performs the first instance of mysquare(), which we will save and reuse numerous times throughout the program.

// a function that accepts a function and returns another
const memoize = (func) => {
  // a collection of results
  const results = {};
  // return a function for the results cache
  return (...args) => {
    //a JSON key to preserve the cached results
    const argsKey = JSON.stringify(args);
    // 'func' should only be used if mysquare has no cached value ()
    if (!results[argsKey]) {
      // mysquare's return value should be saved ()
      results[argsKey] = func(...args);
    }
    // retrieve the results from the cache
    return results[argsKey];
  };
};

//mysquare() should be wrapped with memoize ()
const mysquare = memoize(num => {
    let result = 0;
    for (let i = 1; i <= num; i++) {
        for (let j = 1; j <= num; j++) {
            result++;
        }
    }
    return result;
});

console.log(mysquare(191));
console.log(mysquare(899));
console.log(mysquare(5000));
console.log(mysquare(6467));
console.log(mysquare(7666));

 

When compared to the idea of memoization not being used, the example above executes faster. You may save the cache using a different function, as illustrated above. You might also choose to save the findings in a variable.

Take a look at this example.

const memoizedVal = [];
const mysquare = (num) => {
  if ((memoizedVal[num] == !undefined)) {
    return memoizedVal[num];
  }

  let result = 0;
  for (let i = 1; i <= num; i++) {
    for (let j = 1; j <= num; j++) {
      result++;
    }
  }

  memoizedVal[num] = result;
  return result;
};

console.log(mysquare(191));
console.log(mysquare(899));
console.log(mysquare(5000));
console.log(mysquare(6467));
console.log(mysquare(7666));

Performance Testing

Let's compare the time it takes for a function to execute using the usual function flow to a memoized function.

When the function mysquare() is called, the example below calculates the time it takes.

By Using The Default Flow Of The Function

const mysquare = (num) => {
  let result = 0;
  for (let i = 1; i <= num; i++) {
    for (let j = 1; j <= num; j++) {
      result++;
    }
  }
  return result;
};

console.time("FirstCall");
console.log(mysquare(7467));
console.timeEnd("First call");

// two times the same value
console.time("SecondCall");
console.log(mysquare(7467));
console.timeEnd("SecondCall");

console.time("ThirdCall");
console.log(mysquare(7467));
console.timeEnd("ThirdCall");

 

Output

The time it takes to perform each function gets longer. The execution process is restarted after each function call.

You can practice by yourself with the help of Online Javascript Compiler for better understanding.

By using a Memoized Function

const memoize = (func) => {
  const results = {};
  return (...args) => {
    const argsKey = JSON.stringify(args);
    if (!results[argsKey]) {
      results[argsKey] = func(...args);
    }
    return results[argsKey];
  };
};

const mysquare = memoize((num) => {
  let result = 0;
  for (let i = 1; i <= num; i++) {
    for (let j = 1; j <= num; j++) {
      result++;
    }
  }
  return result;
});

console.time("FirstCall");
console.log(mysquare(7467));
console.timeEnd("FirstCall");

// two times the same value
console.time("SecondCall");
console.log(mysquare(7467));
console.timeEnd("SecondCall");

console.time("ThirdCall");
console.log(mysquare(7467));
console.timeEnd("ThirdCall");

 

When the function is invoked a second time, notice how the execution time drops dramatically. This is because mysquare() was previously cached during the return result.

Output

Memoization With Recursive Functions

When a function calls itself several times, it is referred to as recursion. A break condition will be specified in a function that signals when it should stop calling itself. The idea of looping is used in recursion. When a number iterates numerous times until a given condition is fulfilled, it is said to be in a loop.

A Fibonacci sequence is an excellent example of recursion in action. A Fibonacci sequence predicts the future Fibonacci term by adding two previous numbers in the sequence.

A Fibonacci sequence's initial terms are:

1,1,2,3,5,8,13,...,and so on up to infinity.

Each number is the sum of the two numbers before it. This is how the sequence is put together.

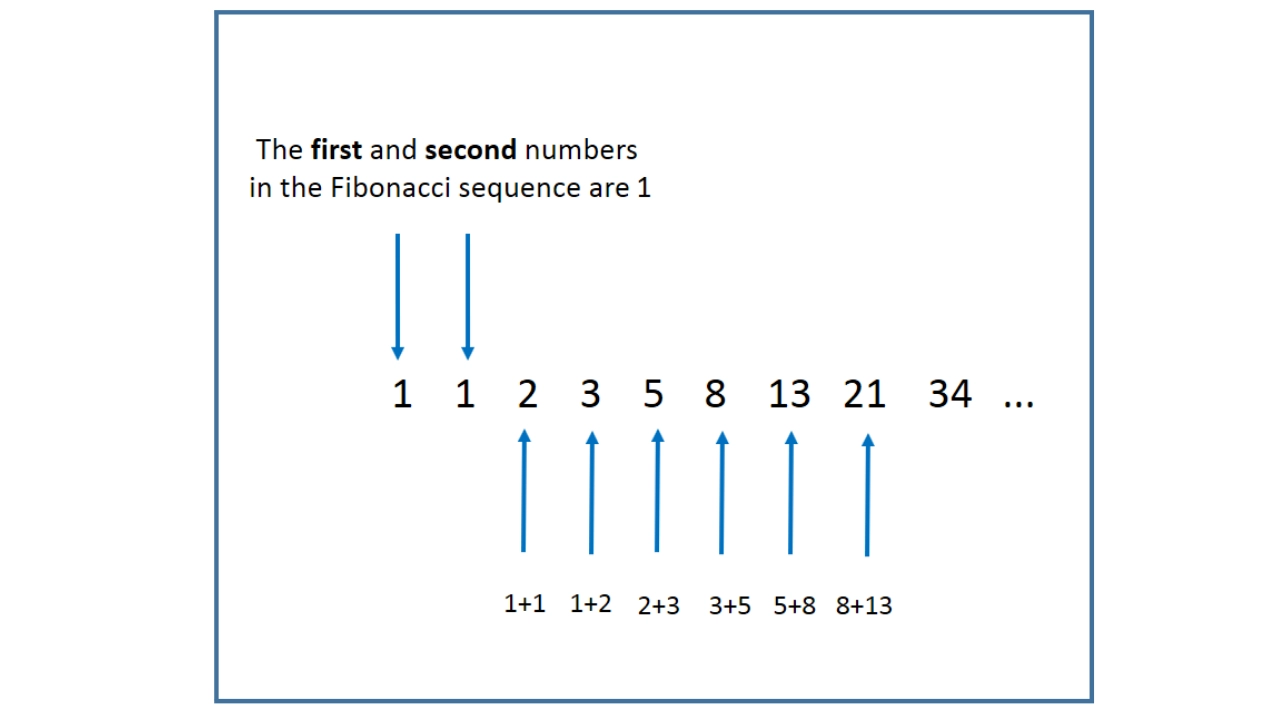
A Fibonacci sequence calculates the same numbers over and over again. This turns into a needless calculation. Furthermore, the application may slow down as you produce more Fibonacci words.

The nth Fibonacci term in the Fibonacci sequence is generated in this Fibonacci example. Keep in mind that the function should run quickly, be well-written, and be stable and trustworthy.

const fibonacci = (n) => {
    //Return the first term 1 if n equals 1.
    if (n == 1) {
      return 1;
    }
    //Return the second term 1 if n equals 2.
    else if (n == 2) {
      return 1;
    }

    //If n is more than two, return the total of the two words before it.
    else 
      return fibonacci(n - 1) + fibonacci(n - 2);
};
//the eighth phrase in the series should be printed
console.log(Fibonacci(8));

 

Output

The program is simple to follow. The eighth period, which is 8, is recorded here.

However, when we try to produce a higher nth Fibonacci term, the program gets more sluggish.

const fibonacci = (n) => {
    // Return the first term 1 if n equals 1.
    if (n == 1) {
      return 1;
    }
    // Return the second term 1 if n equals 2.
    else if (n == 2) {
      return 1;
    }

    // If n is more than two, return the total of the two words before it.
    else 
      return fibonacci(n - 1) + fibonacci(n - 2);
};
// the sixtieth phrase in the series should be printed
console.log(fibonacci(60));

 

Output

This calculation takes around 155319.323 milliseconds to complete.

Behind the scenes, the recursive function operates like this. Take, for example, the sixth term. Fibonacci(5) = Fibonacci(4) + Fibonacci(3) is how the fifth term is computed (3).

Fibonacci(4), on the other hand, must produce fibonacci(3) + fibonacci(4) (2).

Fibonacci numbers must be computed by the software (3). Fibonacci(2) + Fibonacci(1) is called again to return Fibonacci (3).

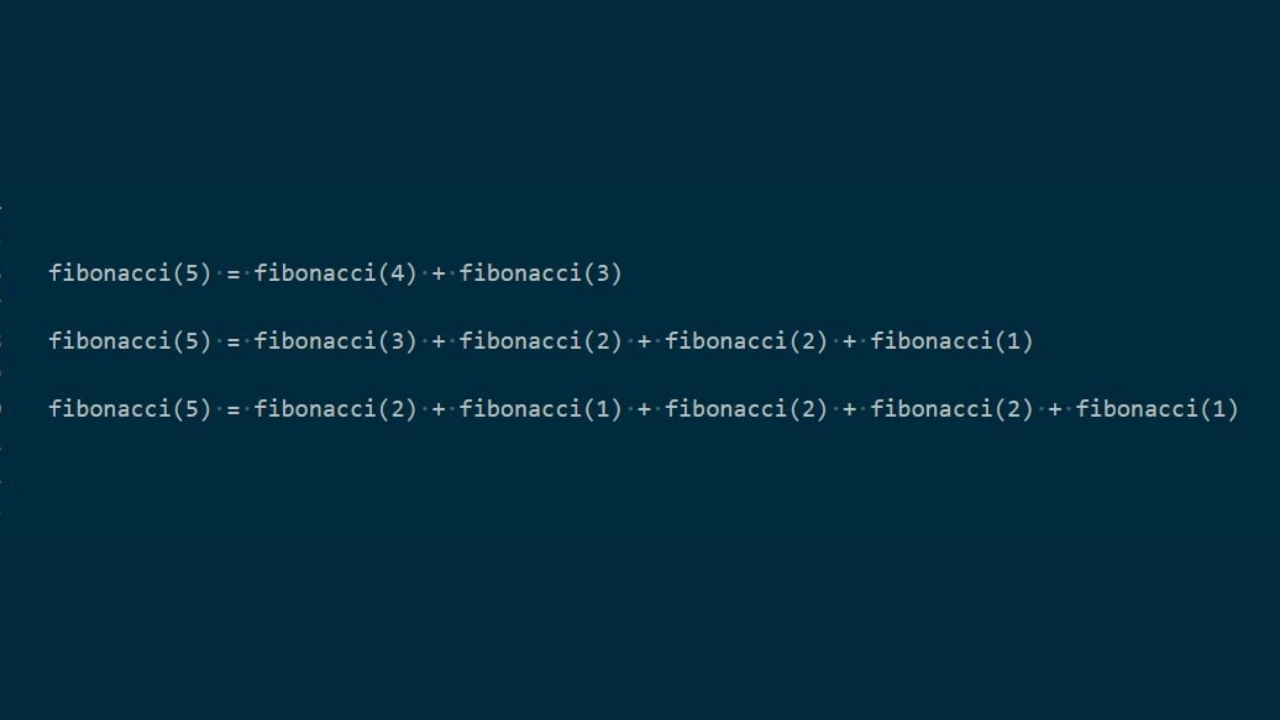
The function repeats itself until the fifth computation term is reached. This is a large number of calculations. When the software returns the previous Fibonacci terms, it will call the Fibonacci calls that were previously called.

You may imagine how many calculations will be required to create the 60th phrase. Because the function repeats itself until the condition of the 60th term is fulfilled, it will be recursive in this situation.

We can instead memorise the function's output.

const memoize = (func) => {
  const results = {};
  return (...args) => {
    const argsKey = JSON.stringify(args);
    if (!results[argsKey]) {
      results[argsKey] = func(...args);
    }
    return results[argsKey];
  };
};

const fibonacci = memoize((n) => {
  // Return the first term 1 if n equals 1.
  if (n == 1) {
    return 1;
  }
  //Return the second term 1 if n equals 2.
  else if (n == 2) {
    return 1;
  }
  // If n is more than two, return the total of the two words before it.
  else 
  return fibonacci(n - 1) + fibonacci(n - 2);
});
//the sixtieth phrase in the series should be printed
console.log(Fibonacci(60));

 

Output

Returning the 60th term with a memoized function takes roughly 4.043ms, which is quicker than the example before.

Every call to a function will be a cache. Fibonacci(5), for example, will just compute Fibonacci(4) + Fibonacci(3) in this situation because the other terms have already been called and cached. Any subsequent calls will not be required to repeat any past calculations.

Check out this problem - Count Ways To Reach The Nth Stair 

Must Read Fibonacci Series in JavaScript,   jquery ajax

Frequently Asked Questions

1.  What exactly do you mean when you say "memoization"?
   It is a technique for speeding up computer systems by caching the results of costly function calls and returning the cached result when the same inputs are used again.
    
2. What is a recursive function?
   A recursive function is a routine that calls itself directly or indirectly in a programming language.
    
3. Why do we need to use memoization in Javascript?
   It's a performance-boosting approach that involves storing the results of function calls. It saves past findings and then retrieves them as needed throughout your programme. This improves CPU performance while reducing execution time.
    
4. When we should not use memoization?
   When the function's output isn't reliant on the input, and the result varies over time, memorising shouldn't be employed.
    
5. When we should use memoization?
   Memoization is a technique for saving values returned by a function so that you don't have to repeat calculations you've already done. This strategy is convenient when we have a frequently called function whose analysis is time-consuming.

Conclusion

In this article, we have discussed the explanation of memoization in Javascript. Memoization is a programming idea that may be used with any language. Its primary purpose is to make your software better. This is most noticeable when software is conducting complex calculations. Memoization will save the results of these computations so that it does not have to work as hard when performing a complex operation that needs a previously completed analysis. This idea has been implemented in several JavaScript libraries, including Async.js, Lodash, Memoizee, Moize, and Fast-memoize.

We hope that this blog has helped you enhance your knowledge regarding memoization in Javascript. If you want to learn more, check out our article on Implement Linear Search and Binary Search in an Array, Debounce and Throttle, and Sort an Array with and without inbuilt methods.

Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. Enroll in our courses and refer to the mock test and problems available; look at the Top 150 Interview Puzzles,  interview experiences and interview bundle for placement preparations.

Do upvote our blog to help other ninjas grow. 

Happy Coding!