The memory-efficient doubly linked list uses only one pointer to traverse the list in both directions. This is achieved by using a bitwise XOR operator to store the front and rear pointer addresses. Rather than storing the actual memory addresses, each node stores the XOR address of the previous and next nodes.
Doubly linked lists data structure are a type of linked lists that can be traversed in both directions, i.e. forward (head to the last node) and backward direction (last node to head). The node of the doubly linked list has three fields: data, address of the next node, and address of the previous node.
The node of a Doubly linked list:

It occupies an extra space for the address of the previous node compared to a simple linked list node as the doubly linked list node contains both the addresses of the previous and the next node. This article will learn about the memory-efficient doubly linked list or XOR linked list, which has only one address or pointer per node using the property of bitwise XOR.
A node of an ordinary doubly linked list contains two addresses: the address of the previous node and the address of the next node, but a node of the memory-efficient doubly linked list contains only one address, the Bitwise XOR of the previous and next address. It can be used as two addresses using an important property of bitwise XOR.
An interesting property of bitwise XOR :
If X ^ Y = Z then Y ^ Z = X and X ^ Z = YFrom the above property, if we have X and Y, we can compute Z. If we have Y and Z, we can compute X, and if we have X and Z, we can compute the value of Y.
We use this property in our doubly linked list for storing the address. Instead of keeping the next and previous addresses, we store the XOR of next and previous addresses.
- Address of the Next Node = Address of Previous Node ^ Address of the current Node.
- Address of the Previous Node = Address of Next Node ^ Address of the current Node.
So if we have a linked list like this:

Nodes of the memory-efficient linked list after using the property of XOR will look like this;
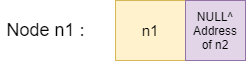
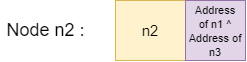


- Node n1: n1->next = NULL(0) XOR address of (n2)
- Node n2: n2->next = address of (n1) XOR address of (n3)
- Node n3: n3->next = address of (n2) XOR address of (n4)
- Node n4: n4->next = address of (n3) XOR NULL(0)
We can traverse the list in both directions in the linked list without any extra previous pointer.
Inserting a node
- We first create a new node.
- Make the next of the new nodes the NULL XOR address(head), i.e. the address of the previous node XOR address of the next node.
- Now, we update the addresses of the next nodes after the head node to the address of the previous node XOR address of the next node.
- Finally, we make the new node the head of the list.
Printing the list
- We create a previous node pointing to NULL and a current node pointing to the head of the list.
- Now, keep repeating the below processes till the end of the list.
- Print the current->data.
- Now, we store the address of the next node as the address of the previous node XOR address of the next node(current->next).
- We update the previous node to the current node and the current node to the next node of the list.
Read about Bitwise Operators in C here.
Code in C++
#include <bits/stdc++.h>
#include <cinttypes>
using namespace std;
class Node
{
public:
int data;
Node* next;
};
Node* XOR(Node* n1, Node* n2)
{
return reinterpret_cast<Node*>(
reinterpret_cast<uintptr_t>(n1)
^ reinterpret_cast<uintptr_t>(n2));
}
void insert_node(Node** head, int new_node_data)
{
Node* newNode = new Node();
newNode->data = new_node_data;
newNode -> next = *head;
if (*head != NULL) {
(*head)-> next = XOR(newNode, (*head) -> next);
}
*head = newNode;
}
void print_linked_list(Node* head)
{
Node* current = head;
Node* previous = NULL;
Node* next;
while (current != NULL) {
cout << current -> data << " ";
next = XOR(previous, current -> next);
previous = current;
current = next;
}
}
int main()
{
Node* head = NULL;
insert_node(&head, 5);
insert_node(&head, 10);
insert_node(&head, 15);
insert_node(&head, 20);
insert_node(&head, 25);
print_linked_list(head);
return (0);
}Output
25 20 15 10 5Complexity Analysis
Time complexity: The time complexity of the insert_node function is O(1), as we haven’t traversed the list.
The time complexity of the print_linked_list function: O(n), where n is the number of nodes in the list, traversing the whole list.
Space complexity: The space complexity of the above solution is O(1) as we need constant extra space.
Check out this problem - Reverse Nodes In K Group




