Introduction
This blog will cover how to merge ‘K’ sorted arrays. Let’s start by looking at the problem statement. There are K Sorted Arrays, each of size N, and you have to merge all these arrays to make one sorted array and return the result.
Also, check out Top Array Coding Interview Questions
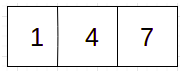
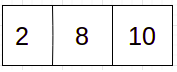
Let’s understand the problem with an example. We are using ‘K’ as 3 in this problem, and we have to return one sorted array after merging all these arrays
Also see, Data Structures
Input -




Recommended: Try the Problem by yourself first before moving on to the solution.
Brute Force Approach
Step 1. Create a resultant array of size N * K.
Step 2. Iterate all the arrays from start to end and insert all the elements in the resultant array.
Step 3. Sort and print the resultant array.
Java Solution
import java.io.*;
import java.util.*;
public class Solution {
public static int[] mergeArrays(int[][] array, int n, int K)
{
// 'temp' variable used for indexing
int temp = 0;
int[] res = new int[n * K];
for (int i = 0; i < K; i++) {
for (int j = 0; j < n; j++)
{
res[temp ++] = arr[i][j];
}
}
// Sorting 'res' array
Arrays.sort(res);
return res;
}
public static void main(String[] args)
{
int[][] arrays = {{ 1, 4, 7},
{ 1, 3, 4},
{ 2, 8, 10 }};
int K = 3;
int n = 3;
// Storing the returned arrays from the 'mergeArrays' function
int[] res = mergeArrays(arrays, n, K, res );
System.out.println("Resultant Merged array is : ");
// Printing all the elements after merging 'K' sorted arrays
for (int a = 0; a < res.length; a++)
{
System.out.print(res[a] + " ");
}
}
}
Output:
Resultant Merged array is
1 1 2 3 4 4 7 8 10 Better Approach
In this approach, we merge arrays in pairs. After the first iteration of merging, we have K/2 arrays. After the second merge, we will have K/4 arrays and so on. We will use recursion to implement this approach for the merge K-sorted arrays problem.
Step 1. Create a function that takes K arrays and returns the resultant array.
Step 2. Implement base condition: if the value of 'K' is 1 then return the array. If ‘K’ contains two, then merge the two arrays and return the array.
Step 3. If the value of K > 2, then divide the group of 'K' elements into equal halves and recursively call the function for each of the halves.
Step 4. Print the resultant array.
Also Read, Prefix Sum Array
Java Solution for Merge K sorted Arrays
import java.util.*;
public class Solution{
public static void merge2Array(int arr1[], int arr2[], int n1,int n2, int arr3[])
{
int i = 0, j = 0, k = 0;
//Merging two arrays and storing them in 'arr3'
while (i<n1 && j <n2)
{
if (arr1[i] < arr2[j])
{
arr3[k++] = arr1[i++];
}
else
{
arr3[k++] = arr2[j++];
}
}
//Leftover elements from an array having size 'n1'
while (i < n1)
{
arr3[k++] = arr1[i++];
}
//Leftover elements from an array having size 'n2'
while (j < n2)
{
arr3[k++] = arr2[j++];
}
}
public static void mergeKSortedArrays(int arr[][], int i, int j, int res[], int n)
{
if(i == j)
{
for(int p = 0; p < n; p++)
{
res[p] = arr[i][p];
}
return;
}
if(j - i == 1)
{
merge2Array(arr[i], arr[j], n, n, res);
return;
}
//Dividing all the elements in the array
int [] output1 = new int[n*(((i + j) / 2) - i + 1)];
int [] output2 = new int[n*(j - ((i + j) / 2))];
mergeKSortedArrays(arr, i, (i + j) / 2, output1);
mergeKSortedArrays(arr, (i + j) / 2 + 1, j, output2);
//function call to merge all the arrays formed using divide calls
merge2Array(output1, output2, n * (((i + j) / 2) - i + 1), n * (j - ((i + j) / 2)), res);
}
public static void main(String[] args)
{
int arrays[][] = {{ 1, 4, 7},
{ 1, 3, 4},
{ 2, 8, 10 }};
int K = arrays.length;
int[] res = new int[arrays[0].length*K];
mergeKSortedArrays(arrays,0,arrays[0].length, res, res[0].length);
System.out.println("Resultant Merged array is : ");
// Printing the elements
for (int i = 0; i < res.length; i++)
{
System.out.print(res[i] + " " );
}
}
}
Output:
Resultant Merged array is
1 1 2 3 4 4 7 8 10
Complexity Analysis of merge K sorted arrays problem:
- Time Complexity: O(N * K * log K) where ‘N’ is the size of arrays and ‘K’ is the total number of sorted arrays. Total levels are log(K) and each level is doing N * K work, so complexity is O(N * K * log K).
- Space Complexity: O(N * K * log k) where ‘N’ is the size of arrays and ‘K’ is the total number of sorted arrays. O(N * K) space is being used at each level and total levels are log(K) which makes it O(N * K * log K).