Merge One Linked List into Another at Alternate Positions

Introduction

In this blog, we will be discussing a linked list data structure problem that has been asked frequently in Interviews.
The problem is to Merge one Linked List into another at alternate positions.

Let us recall what is a linked list.
It is an ordered set of elements, each holding data and a link containing the address to the next element.

To know more about the linked list, refer here. linked-list

Problem Statement

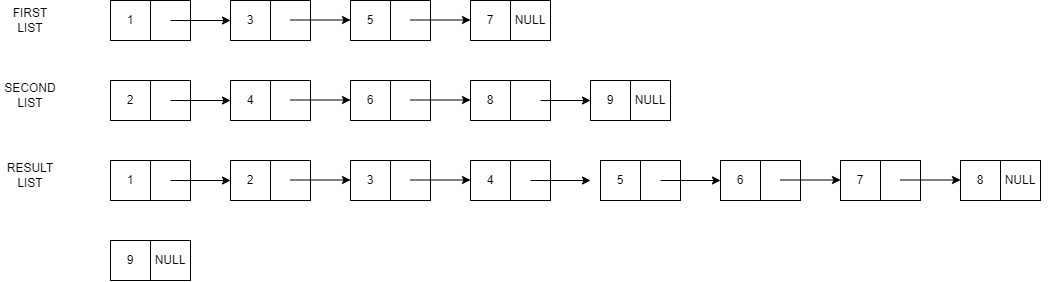
We are given N elements in one linked list and M elements in another linked list. We need to merge both the linked list by adding values from the second linked list at the alternate positions in the first linked list. If the second list is larger than the first one, then after the alternate position ends in the first list, just add the remaining elements.

Sample Example

The given 2 lists are:

Recommended Topic, Floyds Algorithm

Approach

The best approach is to Merge one Linked List into another at alternate positions.

Declare and define two functions. One is to insert a node at the beginning of a linked list and the other to print a linked list. 

⬇

If alternate positions are available in the first linked list, save the next pointers of both the linked list in a variable.

⬇

Make current of q as the next of current of p. Update the next pointer of current of p and q.

⬇

For further iteration, update the current of p and q.

⬇

Update the head pointer of the second list.

Time Complexity: The Time complexity is O(N) Since all elements are traversed only once.

Space Complexity: The Space Complexity is O(1) because no extra space is required.

N: No of elements in each list.

Till now, I assume you must have got the basic conceptual idea of what has been asked in the given problem statement. So, I recommend you first give it a try.
And solve some related problems on the linked list. say for example:
related problems

Don't be sad if you could not Merge one Linked List into another at alternate positions. This is part of the learning process.
Please have a look at the given algorithm, and then again, you must give it a try.

PseudoCode

Algorithm
___________________________________________________________________
procedure merge(Node *p, Node **q):
___________________________________________________________________
1.   Node *p_curr = p, *q_curr = *q
2.   Node *p_next, *q_next
3.   while (p_curr != NULL && q_curr != NULL):
               p_next = p_curr->next
               q_next = q_curr->next;
               q_curr->next = p_next; 
               p_curr->next = q_curr; 
               p_curr = p_next;
               q_curr = q_next;
4. *q = q_curr; 
end procedure
___________________________________________________________________

Implementation in C++

// C++ program to Merge one Linked List into another at alternate positions
#include <bits/stdc++.h>
using namespace std;

class Node
{
	public:
	int data;
	Node *next;
};

//insertion at the beginning
void push(Node ** head_ref, int new_data)
{
	Node* new_node = new Node();
	new_node->data = new_data;
	new_node->next = (*head_ref);
	(*head_ref) = new_node;
}

// printing a singly linked list 
void printList(Node *head)
{
	Node *temp = head;
	while (temp != NULL)
	{
		cout<<temp->data<<" ";
		temp = temp->next;
	}
	cout<<endl;
}

//merging both linked list according to the given condition. Say p be the first linked list and q be the second linked list.
void merge(Node *p, Node **q)
{
	Node *p_curr = p, *q_curr = *q;
	Node *p_next, *q_next;

	// is alternate position is available in p
	while (p_curr != NULL && q_curr != NULL)
	{
		// Saving the very next pointers
		p_next = p_curr->next;
		q_next = q_curr->next;

		// Making current of q as the next of current of p
		q_curr->next = p_next; 
		p_curr->next = q_curr; 

		// Updating current pointers 
		p_curr = p_next;
		q_curr = q_next;
	}

    // Updating head of second list
	*q = q_curr; 
}

int main()
{
	Node *p = NULL, *q = NULL;
	push(&p, 7);
	push(&p, 5);
	push(&p, 3);
	push(&p, 1);

	push(&q, 9);
	push(&q, 8);
	push(&q, 6);
	push(&q, 4);
	push(&q, 2);

	merge(p, &q);

	printList(p);
	printList(q);

	return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input

1 3 5 7
2 4 6 8 9

Output

1 2 3 4 5 6 7 8 
9

Complexity Analysis

Time Complexity: O(n).

Analysing Time Complexity:

Only a single traversal is required.

Space complexity: O(1). No extra space is required