Merge two balanced BSTs

Approach #1 🧑‍💻

We can take the elements of the first balanced BST one by one and start inserting them into the second balanced BST. For this approach, we need to use a self-balancing BST ( AVL tree or red-black tree ). We’ll be using the AVL tree as our self-balancing tree.

You can refer to the below-mentioned articles to learn more about the AVL tree.

• Introduction To AVL Trees
   
• Insertion in AVL Trees
   
• Deletion in AVL Tree

Algorithm

In the below-mentioned algorithm, the INSERT_NODE function is used to insert the node into the AVL tree. For more information, check out the blogs mentioned above.

ALGO_MERGE (TREE_NODE1, TREE_NODE2):
    if TREE_NODE1 is NULL:
        return TREE_NODE2
    
    TREE_NODE2 = ALGO_MERGE(TREE_NODE1->left, TREE_NODE2);
    TREE_NODE2 = INSERT_NODE(TREE_NODE2, TREE_NODE1->DATA);
    TREE_NODE2 = ALGO_MERGE(TREE_NODE1->right, TREE_NODE2);

Implementation in C++ 🧑‍💻

#include <bits/stdc++.h>
using namespace std;

// node class
class Node
{
public:
    int key;
    Node *left, *right;
    int height;


    Node(int key)
    {
        this->key = key;
        left = right = nullptr;
        height = 1;
    }
};

// returns the height of our tree
int getHeight(Node *tree)
{
    if (tree == NULL)
        return 0;
    return tree->height;
}

// left rotate of AVL Tree
Node *leftRotate(Node *t1)
{
    Node *curr = t1->right;
    Node *t2 = curr->left;

    curr->left = t1;
    t1->right = t2;

    t1->height = max(getHeight(t1->left),
                     getHeight(t1->right)) +
                 1;
    curr->height = max(getHeight(curr->left),
                       getHeight(curr->right)) +
                   1;
    return curr;
}

// right rotate of AVL Tree
Node *rightRotate(Node *t1)
{
    Node *curr = t1->left;
    Node *t2 = curr->right;

    curr->right = t1;
    t1->left = t2;

    t1->height = max(getHeight(t1->left),
                     getHeight(t1->right)) + 1;
    curr->height = max(getHeight(curr->left),
                       getHeight(curr->right)) + 1;

    return curr;
}

// returns balance of the tree
int getBalance(Node *tree)
{
    if (tree == NULL)
        return 0;
    return getHeight(tree->left) - getHeight(tree->right);
}

// function to insert the node into tree
Node *insertNode(Node *tree, int key)
{
    if (tree == NULL)
        return new Node(key);

    if (key < tree->key)
        tree->left = insertNode(tree->left, key);
    else if (key > tree->key)
        tree->right = insertNode(tree->right, key);
    else
        return tree;

    tree->height = 1 + max(getHeight(tree->left), getHeight(tree->right));


    int balance = getBalance(tree);

    if (balance > 1 && key < tree->left->key)
        return rightRotate(tree);

    if (balance < -1 && key > tree->right->key)
        return leftRotate(tree);

    if (balance > 1 && key > tree->left->key)
    {
        tree->left = leftRotate(tree->left);
        return rightRotate(tree);
    }

    if (balance < -1 && key < tree->right->key)
    {
        tree->right = rightRotate(tree->right);
        return leftRotate(tree);
    }
    return tree;
}

void preOrder(Node *root)
{
    if (root)
    {
        cout << root->key << " ";
        preOrder(root->left);
        preOrder(root->right);
    }
}

// function to merge tree1 with tree2
Node *mergeTree(Node *tree1, Node *tree2)
{
    if (tree1 == nullptr)
        return tree2;
    tree2 = mergeTree(tree1->left, tree2);
    tree2 = insertNode(tree2, tree1->key);
    tree2 = mergeTree(tree1->right, tree2);
    return tree2;
}

// Driver Code
int main()
{

    // tree 1
    Node *root1 = new Node(5);
    root1->left = new Node(3);
    root1->right = new Node(7);

    // tree 2
    Node *root2 = new Node(12);
    root2->left = new Node(10);
    root2->right = new Node(20);
    root2->left->right = new Node(11);
    root2->right->right = new Node(40);

    // printing tree1
    cout << "Preorder traversal (tree1): ";
    preOrder(root1);
    cout << "\n";

    // printint tree2
    cout << "Preorder traversal (tree2): ";
    preOrder(root2);
    cout << "\n";

    // merging
    root2 = mergeTree(root1, root2);

    // printing merged tree
    cout << "Preorder traversal (after merging): ";
    preOrder(root2);
    cout << "\n";

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output

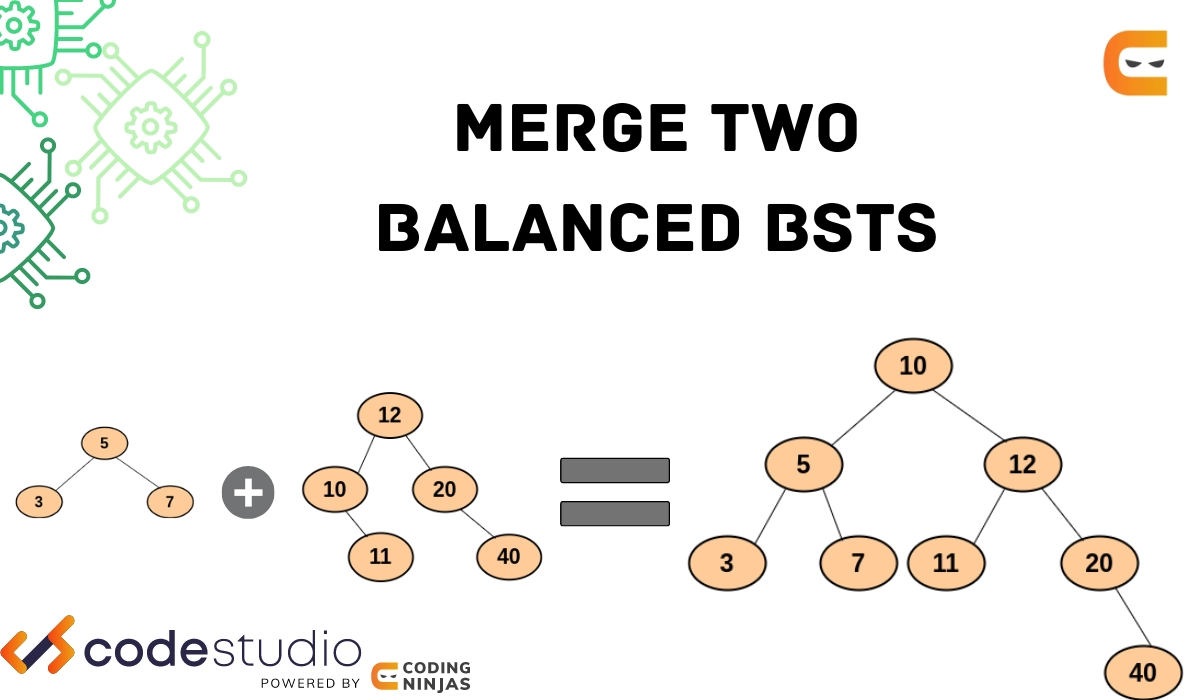
Preorder traversal (tree1): 5 3 7 
Preorder traversal (tree2): 12 10 11 20 40 
Preorder traversal (after merging): 10 5 3 7 12 11 20 40 

Time Complexity ⌛

The number of nodes in the first tree is N and we are inserting all of these nodes into the second tree with M nodes. Insertion operation of self-balancing trees takes O(logX) time where X is the number of nodes in the tree.

So, the overall time complexity of our program would be O(N * logM).
 

Space Complexity 🚀

The space complexity of the above approach is O(logM) where M is the number of nodes in the second input BST. This is because we are inserting nodes in the second tree using recursion. And the size of the recursion stack can go up to O(H) where H = logM is the height of the tree.

You can also read about insertion into bst.

Approach #2 🧑‍💻

We can store the in-order traversal of both BSTs into two different arrays as these two arrays are sorted so we can merge these two arrays into one single Array. Then we can use this sorted merged Array to generate a BST. 

This approach will work even if our original BSTs are not balanced.

Algorithm

1. Create two different arrays and store the in-order traversal of both the trees into these arrays.
    
2. Now you have in order traversal of both the tree into an array. These two arrays will be sorted (as in order traversal of BST is always sorted).
    
3. Merge these two arrays into one single array.
    
4. Now you have one single sorted array with in-order traversal of both the trees. Generate a BST using this single array. Follow the approach explained in “Convert a normal BST to a Balanced BST” article for more clarification regarding this step.

Implementation in C++ 🧑‍💻

#include <bits/stdc++.h>
using namespace std;

// Node class
class Node
{
public:
    int key;
    Node *left, *right;

    Node(int key)
    {
        this->key = key;
        left = right = nullptr;
    }
};

// preorder traversal
void preOrder(Node *root)
{
    if (root)
    {
        cout << root->key << " ";
        preOrder(root->left);
        preOrder(root->right);
    }
}

// function to store the inorder traversal of tree
// into array
void inOrderStore(Node *root, vector<int> &nodes)
{
    if (root == nullptr)
        return;

    inOrderStore(root->left, nodes);
    nodes.push_back(root->key);
    inOrderStore(root->right, nodes);
}

// function to merge two sorted Array into one
vector<int> mergeArray(vector<int> arr1, vector<int> arr2)
{

    // storing size of arr1 and arr2
    int m = arr1.size();
    int n = arr2.size();

    // storing the result into vector
    vector<int> result(m + n, 0);
    int i = 0, j = 0, k = 0;

    // traversing both the arrays
    while (i < m && j < n)
    {
        // Pick the smaller element and put it in result
        if (arr1[i] < arr2[j])
            result[k] = arr1[i++];
        else
            result[k] = arr2[j++];
        k++;
    }

    // If there are more elements in first array
    while (i < m)
    {
        result[k++] = arr1[i++];
    }

    // If there are more elements in second array
    while (j < n)
    {
        result[k++] = arr2[j++];
    }

    return result;
}

Node *convertToBST(vector<int> arr, int start, int end)
{
    // base case
    if (start > end)
        return NULL;

    // getting middle element and making it as root node
    int mid = (start + end) / 2;
    Node *root = new Node(arr[mid]);


    // generating left subtree and assiging it to the
    // left of our root node
    root->left = convertToBST(arr, start, mid - 1);

    // generating right subtree and assiging it to the
    // right of our root node
    root->right = convertToBST(arr, mid + 1, end);

    return root;
}

// function to merge two BSTs into one
// m, n represents the size of tree 1 and 2 respectively
Node *mergeTrees(Node *root1, Node *root2, int m, int n)
{

    // array to store inorder traversal of tree1
    vector<int> arr1;
    inOrderStore(root1, arr1);

    // array to store inorder traversal of tree2
    vector<int> arr2;
    inOrderStore(root2, arr2);

    // Merging sorted array into one
    vector<int> mergedArray = mergeArray(arr1, arr2);

    // Construct a tree from the merged
    // array and return root of the tree
    return convertToBST(mergedArray, 0, m + n - 1);
}

// Main function
int main()
{

    // tree 1
    Node *root1 = new Node(5);
    root1->left = new Node(3);
    root1->right = new Node(7);

    // tree 2
    Node *root2 = new Node(12);
    root2->left = new Node(10);
    root2->right = new Node(20);
    root2->left->right = new Node(11);
    root2->right->right = new Node(40);

    // printing tree1
    cout << "Preorder traversal (tree1): ";
    preOrder(root1);
    cout << "\n";

    // printint tree2
    cout << "Preorder traversal (tree2): ";
    preOrder(root2);
    cout << "\n";

    // merging
    root2 = mergeTrees(root1, root2, 3, 5);

    // printing merged tree
    cout << "Preorder traversal (after merging): ";
    preOrder(root2);
    cout << "\n";

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output

Preorder traversal (tree1): 5 3 7 
Preorder traversal (tree2): 12 10 11 20 40 
Preorder traversal (after merging): 10 5 3 7 12 11 20 40 

Time Complexity ⌛

We are generating the array by doing an inorder traversal on both of our BSTs, this operation takes O(M+N) time, where N and M are the total number of nodes present in our BSTs. After that, we merge both of our generated Arrays into one which takes O(N+M) time. After merging the array we are traversing the merged array only once by finding the mid element and going to the left or right subarray recursively this step takes O(N+M) time as well as the size of our merged array is O(N+M). 

So the overall time complexity of the above program is: O(N+M)

Space Complexity 🚀

We are using two different arrays to store the inorder traversal of both of our BSTs. which takes O(N) and O(M) extra space. So, the overall space complexity of our program would be O(N+M).

Check out this array problem - Merge 2 Sorted Arrays

Frequently Asked Questions 

What are AVL trees?

Adelson-Velskii and Landis trees, or AVL trees, are binary search trees with height-balanced nodes. We can insert and delete at any node as long as we reorganize the tree if the insertion or deletion causes an imbalance.
 

What is a binary tree?

A binary tree is a tree data structure having a maximum of two children. There can only be two children per element in a binary tree, hence we usually refer to them as the left and right children.
 

Why do we perform rotations in an AVL tree?

We calculate the balancing factor (BF) and then rotate each node in accordance with the results to ensure that every node is height-balanced. 

Conclusion

In this article, we have extensively discussed a coding problem in which we have to merge two balanced BSTs into one balanced BST. We have seen a two different approaches to solve this problem.
 

If you think this blog has helped you enhance your knowledge about the above question, and if you would like to learn more, check out our articles 

• Balanced Binary Search Trees 😁
   
• Binary search tree 😎
   
• Deletion in Binary Search Tree 🧐
   
• Unique Binary Search Trees 🤯
   

and many more on our website.

Visit our website to read more such blogs. Make sure that you enrol in the courses we provide, take mock tests, solve problems, and interview puzzles. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations.

Please upvote our blog to help other ninjas grow.

Happy Learning!