Min-Max Algorithm

Introduction

Often, programmers adopt a "recursive leap of faith strategy," which means one can assume the answer to subproblems while solving a complex one. At first, this seems doubtful to the point of being suspect.

But as sir, Samuel Taylor said, “The willing suspension of disbelief for the moment, which constitutes poetic faith,” is needed during recursion. You’ve to trust your solution will give answers to subproblems. This view is often called the holistic view. 

The MinMax Algorithm, which we'll talk about today, is a backtracking strategy used in game theory to discover the player's best move. This algorithm is used in two-players games like tic-tac-toe, chess, etc.

Check out, Backtracking and Recursion

Basic Idea

In the MinMax algorithm, we have two players Maximizer and Minimizer. The job of Maximizer is to maximize the outcome, while Minimizer has to minimize the outcome. MinMax algorithm allows one to look ahead in the possible future states before deciding what moves one should make in the current state.

The solution can typically be visualized as a tree. Each node represents a state in the game and has a statistical value associated with it, which tells how good the state is for one side without making any other move.

Example: In a tic-tac-toe game, the statistical value can be the number of 'X' or '0' to place to make a pair of three.

At each state(Node), one of the two players maximizer or Minimizer needs to make a move to maximize or minimize the outcome. 

Example

For the sake of simplicity, consider a game with four end states and two possible moves at each level. Maximizer has to make a move first, so he's on the tree's root, and Minimizer gets the next level. Each final state has a statistical value. And when its minimizers turn, it will choose the smaller value while the Maximizer will choose the greater value. And they both play optimally.

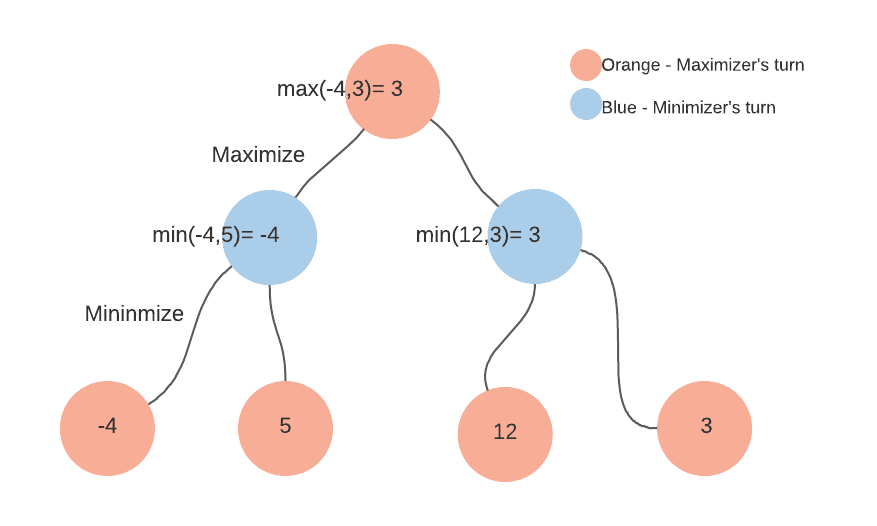
Let’s see how it backtracks to find the most optimal move.

At the root of the tree, its Maximizers turn.

1. Let's say it chooses LEFT.

Now it's the Minimizer's turn.

.

1. Traversing the children, Minimizer chose the minimum value. So it chooses -4. 

Now it backtracks.

     2.   It chooses RIGHT. 

Now it’s the Minimizer’s turn. we are

        1.  Traversing the children minimizer chooses 3

Now it backtracks.

Comparing both values -4 and 3, Maximizer chose 3 as the maximum value.

Now that we've understood the concept, let's try to code it.

Program

• C++

C++

#include <iostream>
using namespace std;

// Function of minmax algorithm will return the maximum value the Maximizer can get when both players play optimally.
int minmax(bool maximizer, int finalStates[], int l, int r)
{
    // If we are on the leaf of the tree. Return the statistical value.
    if (l == r)
    {
        return finalStates[l];
    }

    // Find the middle of the states.
    int mid = (l + r) / 2;

    // If it's Maximizers turn, we have to find the maximum value.
    if (Maximizer)
    {
        return max(minmax(false, finalStates, l, mid), minmax(false, finalStates, mid + 1, r));
    }

    // If it's Minimizers turn Minimum value is returned.
    return min(minmax(true, finalStates, l, mid), minmax(true, finalStates, mid + 1, r));
}

int main()
{
    int n;
    cout << "Enter the number of final states N, where ( N = 2^x ) :";
    cin >> n;
    cout << "Enter the final states : \n";
    int finalStates[n];
    for (int i = 0; i < n; i++)
    {
        cin >> finalStates[i];
    }

    int ans = minmax(true, finalStates, 0, n - 1);

    cout << " Best The Maximizer can get : " << ans << endl;

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input

Enter the number of final states N, where( N=2^x ): 8
Enter the final states :
-2 3 5 12 9 8 -7 -3

Output

Best The Maximizer can get : 3