Minimum nodes to be colored in a graph such that every node has a colored neighbor

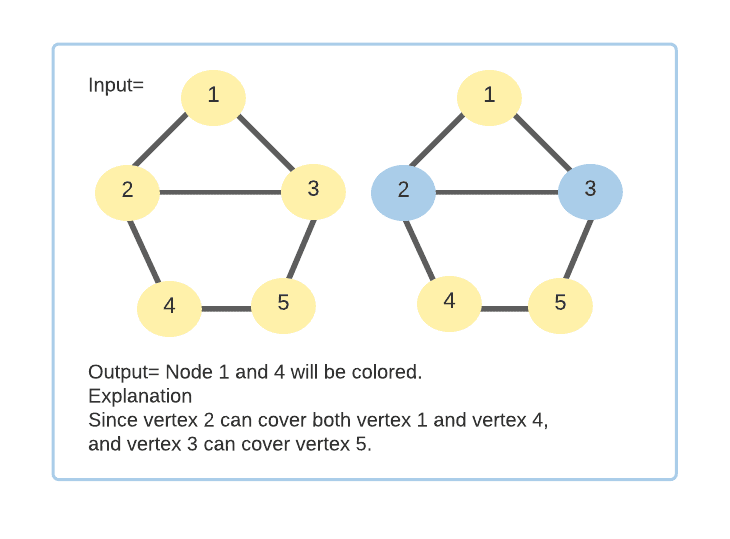
Approach -BFS

The key to solving the problem is to visualize the Graph as a series of layers. Starting with a random source node, we'll divide it into two groups: even and odd. The even group will include nodes with even distances from the source, while the odd group will have nodes with odd distances.

Another thing to observe is that for each node to have one colored node in the neighborhood, we need to color all even nodes or all odd nodes. As a result, we'll pick the group with the fewest nodes and use that as the answer. We’ll be implementing this using BFS. So we’ll create two arrays ODD and EVEN to store the nodes on odd and even levels respectively.

Let's have a look at the algorithm now.

• Initialize a queue ‘Q’ (for BFS) and insert the source node at random into the queue.
• Next, we loop until the ‘Q’ is empty and now we insert nodes into the ‘ODD’ array if the level is odd and in the ‘EVEN’ array if the level is even. Since we only want to know if the level is odd or even, we can even use a boolean variable for tracking the level.
• After we are done with all the nodes return ‘EVEN’ if EVEN.size() is smaller than ODD.size(), else return ‘ODD’.

Now that we’ve worked through the approach, let’s try to code it.

Program

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

// Function that returns minimum nodes to color.
vector<int> minNodesToColor(vector<vector<int>> &graph)
{
   // Number of Nodes.
   int v = graph.size();
   
   // Array to track if the current node is visited or not.
   vector<bool> visited(v, false);
   
   // Queue for BFS traversal.
   queue<int> q;
   
   // Push the source node and mark it visited.
   q.push(0);
   visited[0] = true;
   
   // 'LEVEL' is true if the next level is odd, and false if the next level is even.
   bool level = true;
   
   // Arrays to divide nodes into groups.
   vector<int> even{0}, odd;
   
   // Loop until the queue is not empty.
   while (!q.empty())
   {
       int sz = q.size();
       
       // We traverse all the current level nodes together.
       while (sz--)
       {
           // Popping out one node.
           int curr = q.front();
           q.pop();
           
           // If the next level is odd, we traverse all its neighbors, and one which is not visited is inserted into the 'ODD' group.
           if (level)
           {
               for (int &currFriend : graph[curr])
               {
                   if (!visited[currFriend])
                   {
                       odd.emplace_back(currFriend);
                       visited[currFriend] = true;
                       q.push(currFriend);
                   }
               }
           }
           
           // If the next level is even, we insert nodes into the 'EVEN' group.
           else
           {
               for (int &currFriend : graph[curr])
               {
                   if (!visited[currFriend])
                   {
                       even.emplace_back(currFriend);
                       visited[currFriend] = true;
                       q.push(currFriend);
                   }
               }
           }
       }
       
       // Last, we flip the boolean level.
       level = !level;
   }
   // Return the group with minimum size.
   return (even.size() < odd.size() ? even : odd);
}

int main()
{
   // Taking user input.
   int v, e;
   cout << "Enter the Number of vertices: ";
   cin >> v;
   vector<vector<int>> graph(v);
   cout << "Enter the number of edges: ";
   cin >> e;
   cout << "Enter all pairs U and V:\n";
   int x, y;
   for (int i = 0; i < e; i++)
   {
       cin >> x >> y;
       graph[x].emplace_back(y);
       graph[y].emplace_back(x);
   }
   
   // Calling the 'minNodesToColor()' Function that returns minimum nodes to color, so every node has a colored neighbor.
   vector<int> minList = minNodesToColor(graph);
   cout << "Nodes that are to be colored are: ";
   for (int i = 0; i < minList.size(); i++)
   {
       cout << minList[i] << " ";
   }
   cout << endl;
   return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input

Enter the number of vertices: 7
Enter the number of edges: 7
Enter all pairs of U and V:
0 1
0 2
2 3
2 4
2 6
3 4
4 5

Output

Nodes that are to be colored are: 1 2 5

Time Complexity

O(V), where ‘V’ is the number of vertices in the graph.

Since we are traversing every node exactly once, so the time complexity is O(V).

Space Complexity

O(V).

Since we are creating three vectors and a queue of size ‘V’, space complexity is O(V).

Key Takeaways

Mostly all Graph problems can be solved using BFS or DFS Algorithm. Hence, both these algorithms are fundamental, and you should know them simply because it’s 2 + 2 for graphs.

I hope you had fun reading this blog. Check other such exciting blogs on Coding Ninjas Studio.

Coding NIjas has also released a new Mock Test Series for cracking top tech companies.

Thanks for reading.