Example
Let's begin with the following example.
arr[] = [1, 15, 18, 3, 14, 18, 5]
k = 9
arr[] = [1, 15, 18, 3, 14, 18, 5].
After swapping 15 and 3 the new updated array,
arr[] = [1, 3, 18, 15, 14, 18, 5].
After swapping the first occurrence of 18 and 5,
arr[] = [1, 3, 5, 12, 14, 18, 18].
Now, all elements less than or equal to 9 are together.
So, the minimum number of swapping required is 2. Hence the answer is 2.
Algorithm
Let’s see the algorithm for the given problem statement. To get the solution, we have two possible ways.
Method 1
The very first method is the Brute-force method. This algorithm consists of the following steps:
- The first is the most intuitive: count the numbers less than k;
- then go to each subarray and start swapping with those larger than k.
Method 2
This is an efficient algorithm. It uses two pointers + sliding window approach.
The main steps of this algorithm are as follows:
- Get the total number of elements that are less than or equal to k.
- Calculate the total number of elements that are greater than k.
- Set output to a smaller value(smaller count of elements).
-
From i = 0 and j = count, traverse the array.
If array[i] is larger than the value of k, reduce the value of smaller by one.
If array[j] is larger than the value of k, increase smaller by one.
Find the minimum between the output and the smaller and save it to the output.
- Print the final output.
Working
The concept is to group all of the elements<= k together; this group of elements can be located anywhere in the array as a subarray. The window size will be determined by the count of elements <= k.
We'll now glide from the beginning to the end of the array, window size=number of elements less than or equal to k. The goal is to locate the window with the smallest elements>k.
Here we are taking an example to understand the working of the algorithm using the technique of two-pointers and sliding windows.
Given: [1, 15, 18, 3, 14, 18, 5] and k = 9
Number of elements < = k is 3 i.e. = { 1, 3, 5}
So, if we want these three items to be together, we'll look at all windows of size 3 with the fewest elements > 9.
Let's begin sliding the window,
[ 1, 15, 18, 3, 14, 18, 5 ] => Here 2 elements are greater than 9 i.e.{ 15, 18 }
[ 1, 15, 18, 3, 14, 18, 5 ] => Here 2 elements are greater than 9 i.e.{ 15, 18 }
[ 1, 15, 18, 3, 14, 18, 5 ] => Here 2 elements are greater than 9 i.e.{ 18, 14 }
[ 1, 15, 18, 3, 14, 18, 5 ] => Here 2 elements are greater than 9 i.e.{ 14, 18 }
[ 1, 15, 18, 3, 14, 18, 5 ] => Here 2 elements are greater than 9 i.e.{ 14, 18 }
Now, arr[] = {1, 15, 18, 3, 14, 18, 5}
Swap 15 and 3 => arr[] = {1, 3, 18, 15, 14, 18, 5}
Swap 18 and 5 => arr[] = {1, 3, 5, 15, 14, 18, 18}
Now, all elements less than or equal to 9 are together. So the number of minimum swaps required is 2.
Also see, Rabin Karp Algorithm.
Implementation
Here is the implementation of the algorithm in different programming languages.
Approach 1( C++)
The given code is the implementation of our efficient algorithm in C++ language.
Code
#include <iostream>
using namespace std;
int minimumSwap(int arr[], int n, int k)
{
// count of elements <= k
int cnt = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++cnt;
// count of unwanted elements in window of size cnt.
int ucnt = 0;
for (int i = 0; i < cnt; ++i)
if (arr[i] > k)
++ucnt;
int ans = ucnt;
for (int i = 0, j = cnt; j < n; ++i, ++j)
{
if (arr[i] > k)
--ucnt;
if (arr[j] > k)
++ucnt;
ans = min(ans, ucnt);
}
return ans;
}
int main()
{
int arr[] = {1,15,18,3,14,18,5};
int n = sizeof(arr) / sizeof(arr[0]);
int k = 9;
int result = minimumSwap(arr, n, k);
cout <<" The Minimum no of swaps required is:" <<result;
return 0;
}

You can also try this code with Online C++ Compiler
Output

Approach 2( Python 3)
The given code is the implementation of our algorithm in Python language.
Code
def minimumSwap(arr, n, k) :
#count of elements <= k
cnt = 0
for i in range(0, n) :
if (arr[i] <= k) :
cnt = cnt + 1
# count unwanted elements in window of size 'cnt'
ucnt = 0
for i in range(0, cnt) :
if (arr[i] > k) :
ucnt = ucnt + 1
# Initialize ans
ans = ucnt
j = cnt
for i in range(0, n) :
if(j == n) :
break
# Decrement count
if (arr[i] > k) :
ucnt = ucnt - 1
# Increment count
if (arr[j] > k) :
ucnt = ucnt + 1
ans = min(ans,ucnt)
j = j + 1
return ans
# Driver code
arr = [1, 15, 18, 3, 14, 18, 5]
n = len(arr)
k = 9
print ("The minimum number of swaps required is:",minimumSwap(arr, n, k))

You can also try this code with Online Python Compiler
Output

Approach 3( C#)
The given code implements our algorithm using the C# language.
Code
using System;
class Coding {
static int minimumSwap(int []arr, int n, int k) {
int cnt = 0;
for (int i = 0; i < n; ++i)
if (arr[i] <= k)
++cnt;
int ucnt = 0;
for (int i = 0; i < cnt; ++i)
if (arr[i] > k)
++ucnt;
// Initialize ans
int ans = ucnt;
for (int i = 0, j = cnt; j < n; ++i, ++j) {
if (arr[i] > k)
--ucnt;
if (arr[j] > k)
++ucnt;
ans = Math.Min(ans, ucnt);
}
return ans;
}
// Driver code
public static void Main()
{
int []arr = {1, 15, 18, 3, 14, 18, 5};
int n = arr.Length;
int k = 9;
Console.WriteLine(minimumSwap(arr, n, k));
}
}
Output
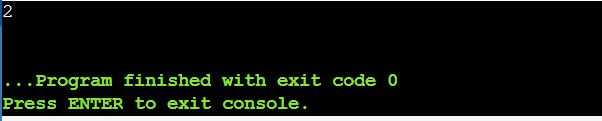
Complexity Analysis
We have discussed various approaches in different languages of our Algorithm. Now let’s analyse the space and time complexity of the algorithm.
Time Complexity
- The time complexity for the brute-force algorithm is O(n2).
- The time complexity for the efficient algorithm is O(n), where n is the number of elements in the array.
Space Complexity
The efficient algorithm's time complexity is O(1), as no extra space is required.
Check out this problem - Next Smaller Element
Frequently Asked Questions
In an array, what is the Peak element?
An array element that is not smaller than its neighbours is called the peak element. For example, in an array of { 8,7,10,15,9} ,the array's peak element is 15.
What's the best way to figure out how large an array is?
The sizeof operator can be used to determine how big your array is in bytes. We may divide the overall size of the array by the size of the array element to find the number of elements in the array.
How many different kinds of arrays are there?
Arrays can be classified into three types:
- indexed arrays,
- multidimensional arrays, and
- associative arrays.
In an array, how do you find the length of a string?
Simply take the string or array and follow it with a dot and the keyword length to obtain the size. This determines the string or array's length. For example, we can find the length as arr.length for an array named “arr.”
Conclusion
This blog discussed how we could find the minimum swaps required to bring all elements together less than or equal to a given number.
We have discussed,
- Example of the method.
- Algorithm for the solution.
- Working of the Algorithm.
- Implementation of the Algorithm.
- Complexity Analysis of the Algorithm.
This blog is related to array rearrangement, so it is advised to check these articles on rearranging an array and rearranging an array such that arr[i] = i. You can visit Coding Ninjas Studio for more Coding Interview Questions.
Recommended Problems -
To learn more about array rearrangement problems, visit the Array rearranging Problems at Coding Ninjas Studio.
Head over to our practice platform Coding Ninjas Studio to practice top problems, attempt mock tests, read interview experiences, interview bundle, follow guided paths for placement preparations, and much more!!
We wish you Good Luck! Keep coding and keep reading Ninja!!






