Introduction
Binary Trees are popular Data Structures and have a wide range of applications throughout various fields. Binary Trees are also important when it comes to interviews with top tech companies. A mastery of Binary Trees could help us solve a lot of problems. In this article, we are going to take a look at one such problem.
Before Diving into the question, let’s first understand what a binary tree is.
A binary tree is a hierarchical data structure in which each node has at most two children, generally the left child and right child. The topmost node in the tree is called the root. Each node contains three components:
- Pointer to left subtree
- Pointer to right subtree
- Data element
Let us now understand the following problem on binary trees. The problem statement is as follows - Given a binary tree, you need to construct a tree that is the same as the mirror image of the given tree.
In the image below, we have a tree in which we have created the mirror image of the same.
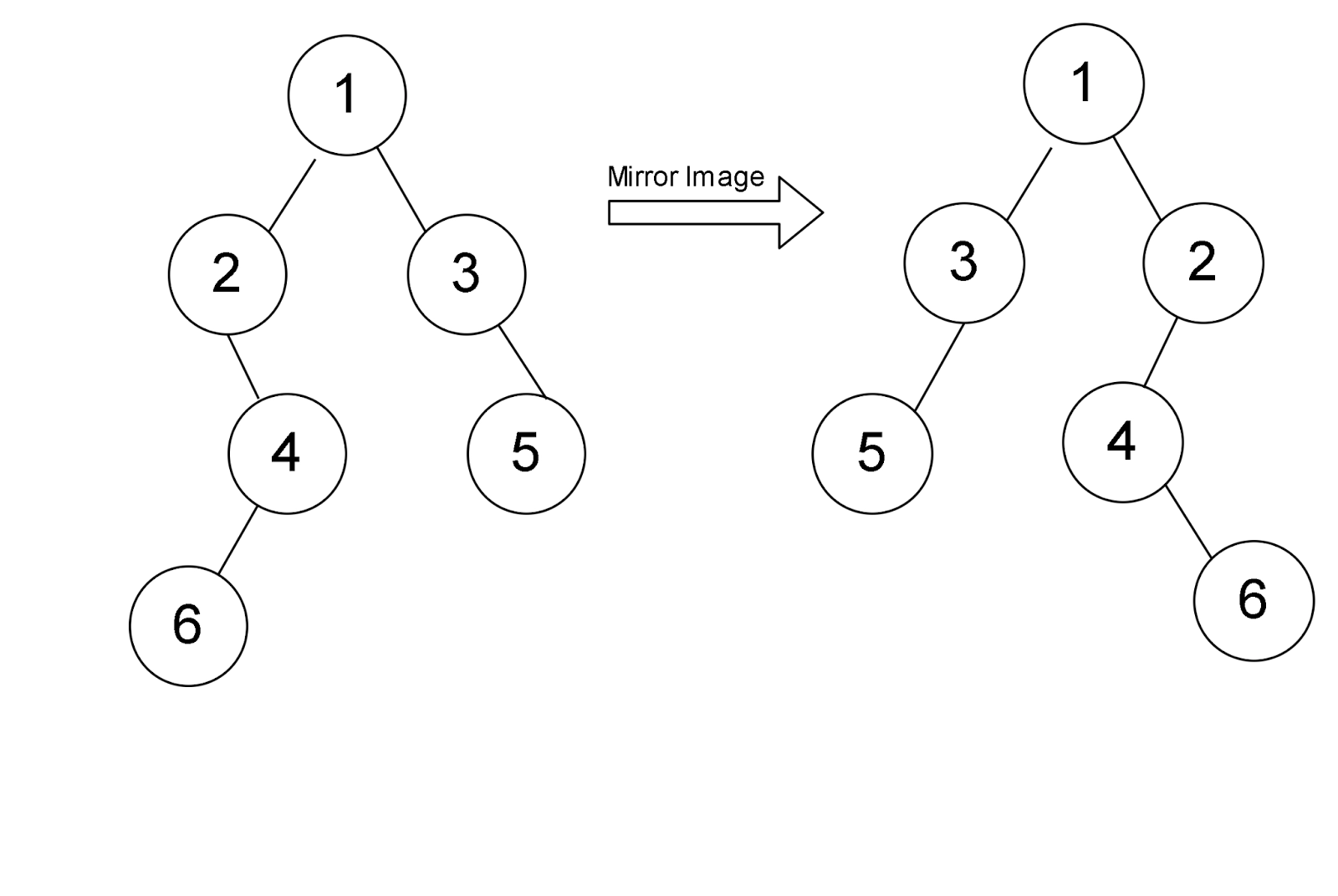
Now, if we look at the example, we are given a tree present on the left-hand side, and we have to construct a tree like the one present on the right-hand side from scratch. Now, let’s have a look at the algorithm to understand the solution to the problem.
Algorithm
One of the approaches can be to construct a new tree that will be the mirror image of the given tree. We can write a recursive algorithm that takes the root of the original tree and the mirror tree as arguments.
The steps for the recursive approach for constructing a mirror tree:
- Set the root of the mirror tree equal to the root of the original tree.
-
Recursively call the function for creating the left and right child of the mirror tree.
- Set the left child of the current node in the mirror tree as the right child of the current node in the original tree.
- Set the right child of the current node in the mirror tree as the left child of the current node in the original tree.
-
If the current node in the original tree is NULL, simply return.
Observing the above steps carefully we can say that the above steps are equivalent to swapping the left and right child of the current node in the given original tree and recursively calling the function for left and right child.
We can rewrite the simple recursive algorithm with the following steps.
- For every node, swap the address for the left and right nodes.
- Call recursive functions for the left and right subtree.
- Repeat step 1
- We will stop the recursion when we reach the leaf node. I.e when both the left and right child are null.
Let us look at the code below to understand how to create a Mirror tree from the given binary tree:
Must Read Recursive Binary Search.
Code in C++
#include <iostream>
using namespace std;
struct Node{
int data;
Node*left;
Node*right;
Node(int x){
data = x; Node* left = NULL; Node*right = NULL;
}
};
// this function simply prints the inorder traversal of the given tree
void inorder(Node* root)
{
if (root == NULL)
return;
inorder(root->left);
cout <<" "<< root->data;
inorder(root->right);
}
// Note - here we have passed the address of the mirror tree.
void MirrorTheTree(Node* root, Node** mirror)
{
// this is the base case when Node is null
if (root == NULL) {
mirror = NULL;
return;
}
// we have created a new Node here for the mirror tree
*mirror = new Node(root->data);
// we are now calling the left and the right subtrees
MirrorTheTree(root->left, &((*mirror)->right));
MirrorTheTree(root->right, &((*mirror)->left));
}
int main()
{
Node* tree = new Node(1);
tree->left = new Node(2);
tree->right = new Node(3);
tree->left->right = new Node(4);
tree->left->right->left = new Node(6);
tree->right->right = new Node(5);
// Print inorder traversal of the input tree
cout <<"Inorder of the given tree: ";
inorder(tree);
Node* mirrorTree = NULL;
MirrorTheTree(tree, &mirrorTree);
// Print inorder traversal of the mirror tree
cout <<"\nInorder of the given tree: ";
inorder(mirrorTree);
return 0;
}
Output :
|
Inorder of the given tree: 2 6 4 1 3 5 Inorder of the given tree: 5 3 1 4 6 2 |
Time Complexity - O(N)
Since we are traversing every node once, the time complexity to create the mirror tree from the given binary tree is of the order N, where N is the number of nodes present in the tree.
Space Complexity - O(1)
As we are not using any type of extra space, the space complexity for creating the mirror tree from the given binary tree is of the order of O(1).





