Modify a Binary Tree to get Preorder Traversal using Right Pointers only

Introduction

Binary trees are one of the most prominent data structures discussed in technical interviews. It holds such importance as it tends to test the candidate’s knowledge of not only the data structures but also get an idea of this logical and thinking ability. 

So, in this article, we will discuss the problem: Modify a binary tree to get preorder traversal using right pointers only in detail. 

Also See, Binary Tree Postorder Traversal.

Problem Statement 

Given a binary tree, write a function that modifies it in such a way that its preorder traversal can be obtained using only the right pointer.  

Explanation of the problem 

You will be given a binary tree. You have to rearrange its nodes such that using its right pointers, only preorder traversal of the original tree can be obtained.  

If a binary tree is as follows: 

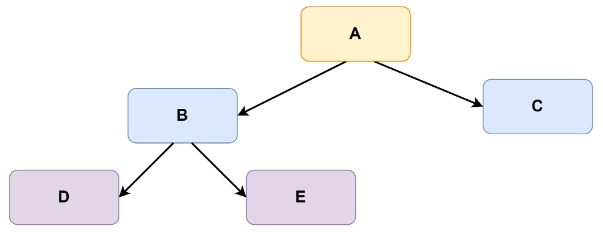
Then, the preorder traversal will be A B D E C. 
To get a preorder traversal of a binary tree, the rule used is -visit the node, then the left child, and finally the right child.

The question does not, in any sense, says that while modification left pointer and right pointer both can be used. It is just that, after modification, only the right pointers have to be used. 

Sample Example 

For the given binary tree: 

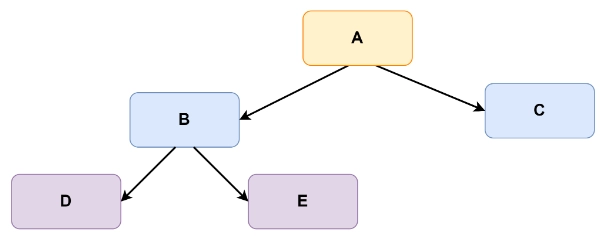
The binary tree after modification will be as follows:

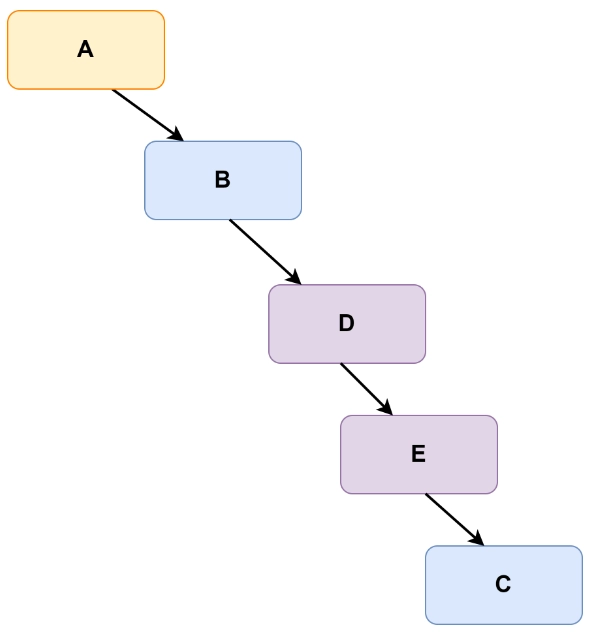
Approach to the problem 

According to the question, you are supposed to think of how you can rearrange the nodes of the binary tree so that after rearrangement, only the right pointers are used when preorder traversal is performed. After modification, the usage of the left pointer should not be required. And preorder traversal has been explained earlier in this article.

So, if you observe carefully, it is like making the left child of a node its right child, and then the right child of the considered node is made the right child of the rightmost child of the left child of the considered node. 

If a node does not have a right child, the left child can be made the right child.

Another observation is that it always results in a right-skewed tree.

It might have been a little confusing at this point. To make it clear, let us take an example.  

If we have the following binary tree:

Going as per what we have described above, 

Step 1: 

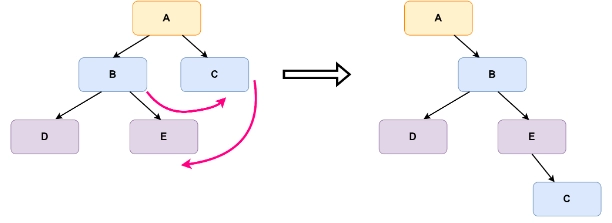
Step 2:

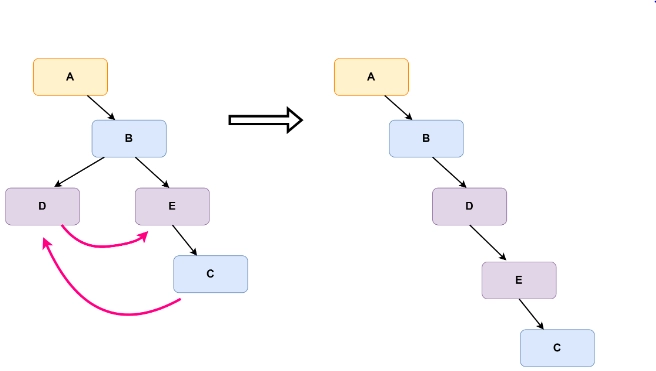
It was a small binary tree, so it took only two steps. Although the check would be done on further nodes, but no more modifications will happen.   

Steps of the approach

1. For a given node in a binary tree:
   1.1. If the node has no right child, then move the left the child to the right
   1.2. If a right child is present, then make it the right child of the right-most of the original left subtree.  
2. Repeat step 1 till you reach the node with no child at all. 

Implementation in C++ 

#include <bits/stdc++.h>
using namespace std;

class node		//Class of node
{
	public:
    	char val;
    	node* left,* right;
};

node* new_node(char value)		//Creating a new node
{
	node* t=new node;
	t->val=value;
	t->left->right==NULL;
	return t;
}


node* modification(node* parent)	 //Modifying the binary tree
{
	node* right=parent->right;
	node* right_most=parent;


	if(parent->left)
	{
		right_most=modification(parent->left);
		parent->right =parent->left;
		parent->left=NULL;
	}
	if(!right)
		return right_most;

	right_most->right=right;
	right_most=modification(right);
	return right_most;
}

void preorder_traversal(node* root)		//Preorder only using right pointer
{
	while(root!=NULL) 
	{
		cout<<root->val<<" ";
		root=root->right;
	}
}

int main()
{
	return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input: 

node* root=new_node('A');
root->left=new_node('B');
root->right=new_node('C');
root->left->left=new_node('D');
root->left->right=new_node('E');
modification(root); 
cout<<"Preorder traversal is: ";
preorder_traversal(root);

Output:

Preorder traversal is: A B D E C  

Complexity Analysis 

Time Complexity: O(n) 
Here, n is the total nodes in the binary tree. 

Space Complexity: O(n)
The recursion stack takes up the auxiliary space. 

Note: The above approach is recursive. The same thing can be implemented in an iterative manner. 

For that, we need to maintain a variable, let us say ‘p’,  to store the previous node of the preorder traversal. Every time the node makes its right to the previous one, the p is equal to the current node. Finally, we will have a linked list whose first element is the root, then the left child, then the right, and the same continues. You can read more about Iterative Preorder Traversal here.

Iterative Implementation in C++

#include<bits/stdc++.h>
using namespace std;
 
class node		//Class of new node
{
    public:
        char val;
        node* left,*right;
};

node* new_node(char value)		//Creating a new node
{
    node* t=new node;
    t->val=value;
    t->left=NULL;
    t->right=NULL;
    return t;
}
 
void modification(node* parent)		//Modifying the binary tree
{
    if(parent==NULL)
        return;
 
    stack<node*> nodes;
    nodes.push(parent);
    node* p=NULL;
    while(nodes.empty()==false) 
    {
        node* t=nodes.top();
        nodes.pop();
        if(t->right)
            nodes.push(t->right);
        if (t->left)
            nodes.push(t->left);
 
         if(p!=NULL) 
         {
            p->right=t;
        }
        p=t;
    }
}

void preorder_traversal(node* root)		//Preorder traversal using right pointer
{
    while(root!=NULL)
    {
        cout<<root->val<<" ";
        root=root->right;
    }
}

int main()
{ 
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input:

node* root=new_node('A');
root->left=new_node('B');
root->right=new_node('C');
root->left->left=new_node('D');
root->left->right=new_node('E');
 
cout<<"The preorder traversal is: "
modification(root);
preorder_traversal(root);

Output:

The preorder traversal is: A B D E C  

Complexity Analysis 

Time Complexity: O(n) 
Here, n is the total nodes in the binary tree. 

Space Complexity: O(n)
The stack takes up the auxiliary space. 

Check out this problem - Mirror A Binary Tree