Monty Hall Problem

Introduction 

Puzzles are a good measure of one's analytical skills and lateral thinking. Many product-based companies ask the puzzles to help them filter candidates based on their real-world problem-solving skills to approach a problem they have not seen before.

A puzzle may have multiple solutions. The interviewer is generally interested in the candidate's approach to solving the mystery and the approach to build and think creatively for the answer to the puzzle.

Puzzle Description

Suppose you’re on a show, and you’re given the selection of 3 doors: Behind one door is a car, at the back of the opposite, are goats. You choose a door, say number1, and the host, who is aware of what’s at the back of the doors, opens every other door, say number3, which has a goat. He then says to you, “Do you need to choose door №2?” Is it to your benefit to replace your choice?

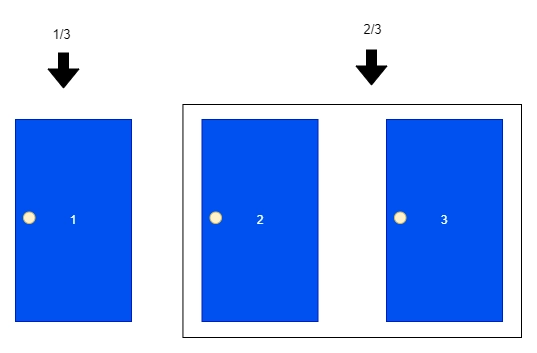
Solution

Most people could say that when one door is discovered, you then definitely have the most straightforward 2 picks left and consequently, your possibilities of prevailing are half off or 50%, and so it wouldn’t remember in case you stay with your choice or switched doors.

If you switch, your chance of winning will be more even though reasonably maximum human beings pick out to stay.
Let us consider the sport display (Let’s Make a Deal) from the suggested factor of view, the show and the suggests host (Monty) is aware of in which there's a goat and in which there isn’t a goat and consequently is mindful of which door the prize is in the back of. So, we're given three doors (Door #1, Door #2, and Door#3). Behind the primary door is a goat, in the back of the second door is a car (our prize) and in the back of the 0.33 door is any other goat.

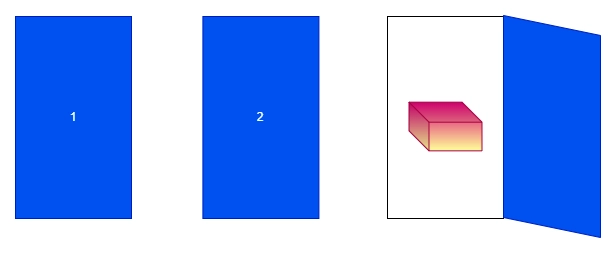
Suppose the contestant chooses Door #1, then the host well-known shows Door #three (the goat) because the host is aware that Door #2 incorporates the prize car. In this situation, it is ideal for the contestant to interchange. If the contestant/participant switches, the contestant might win the prize. If the contestant/participant did NOT transfer, the contestant might lose the award.

Suppose the contestant chooses Door #2, then the well-known host shows both Door #1 or Door #three. In this situation, it's miles horrific to interchange for the contestant. If the contestant/participant switches, then the contestant might lose the prize. If the contestant/participant did NOT transfer, then the contestant might win the award.

Suppose the contestant chooses Door #three, then the host well-known shows Door #1. In this situation, it is ideal for the contestant to interchange. If the contestant/participant switches, then the contestant might win the prize. If the contestant/participant did NOT transfer, then the contestant might lose the award.

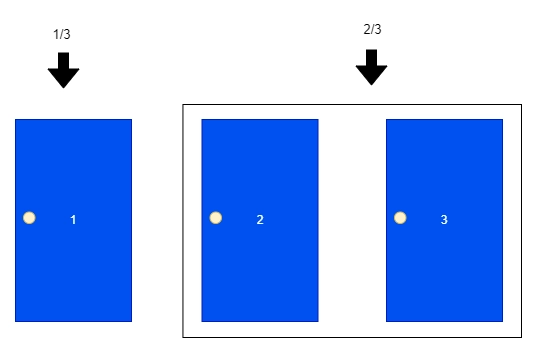
In the above scenario, we are able to effortlessly see that if the contestant had switched, then the contestant might’ve gained 2/three or approximately 66.66% of the time and misplaced the simplest 1/three or approximately 33.33% of the time. If contestant decides to stay, then the contestant might’ve gained 1/three or approximately 33.33% of the time and misplaced 2/three or approximately 66.66% of the time

Let’s examine the possibility of NEVER switching. There are three doorways, and 1 of the three doorways incorporates the car, your favored prize, at the same time as 2 of the three doorways incorporate the undesired prize (the goat). If staying in the choice by contestant's intestine feeling and pick to by no means transfer, then the possibility of prevailing is 1/three, and their probability of dropping is 2/three.

After staying together along with your authentic choice: Probability( Winning) = P(W) = 1/3

After staying together along with your authentic choice: Probability (Losing) = P(L) = 2/3

Now let’s check the chance of ALWAYS switching. Let’s consider how you'll win in case you constantly change. Fig. 1 suggests three doorways containing the goat, car, and goat. If you picked door #1, the host would display you door #three, and also, you must transfer. If you decide on door #three, the host will show you door #1, and also, you must move. So in case you chose an incorrect door (an entry containing a goat) and transfer, you constantly win, and if you selected the door that included the prize after which switched, you'd lose.

Let’s examine a scenario. Assume the prize is in the back of door #2 and goats are in the back of doorways #1 and #three.

Scenario #1 for continually switching:

1. You pick outdoor #1
2. The host opens door #three because the prize is at the back of door #2 and asks in case you need to exchange.
3. You determine to exchange to door #2
4. YOU WIN!

Scenario #2 for continually switching

1. You pick door #2
2. The host opens door #three or door #1 because the prize is at the back of door # 2 and asks in case you need to exchange.
3. You determine to exchange to door #1 or door #three
4. YOU LOSE.

Scenario #3 for continually switching

1. You pick door #three
2. The host opens door #1 because the prize is at the back of door #2 and asks in case you need to exchange.
3. You determine to exchange to door #2
4. YOU WIN!

From the feasible eventualities above in which the prize becomes at the back of door #2, and you opted to switch continually, you would’ve gained 2/three instances from switching and misplaced 1/three instances for changing or vice versa. You would’ve achieved 1/three of the time using sticking together along with your preference and lost 2/three of the time for sticking together along with your selection.

After switching unique preference: Probability ( Winning) = P(W) = 2/three

Probability (Losing) = P(L) = 1/three

By switching doorways on this case, your opportunity of triumphing is 2/three, and your chance of dropping is one/three. Another manner of considering it is, if you pick out to exchange, you double your probabilities of triumphing or boom your possibilities of triumphing with the aid of using 1/three or approximately 33.33%.

Implementation in C++

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
int main()
{
    int games1 = 0;
    int stayWins1 = 0;
    int switchWins1 = 0;
    int chosenDoor1;
    int remainingDoor1;
    int revealedDoor1;
    int winningDoor1;
    int choice;

    srand(time(NULL));
    chosenDoor1 = rand() % 3 + 1;
    winningDoor1 = rand() % 3 + 1;

    do
    {
        do
        {
            revealedDoor1 = rand() % 3 + 1;
        } while (revealedDoor1 == chosenDoor1 || revealedDoor1 == winningDoor1);

        do
        {
            remainingDoor1 = rand() % 3 + 1;
        } while (remainingDoor1 == chosenDoor1 || remainingDoor1 == revealedDoor1);

        choice = rand() % 2 + 1;
        if (choice == 1)
        {
            if (chosenDoor1 == winningDoor1)
            {
                stayWins1++;
            }
        }
        if (choice == 2)
        {
            chosenDoor1 = remainingDoor1;
            if (chosenDoor1 == winningDoor1)
            {
                switchWins1++;
            }
        }
        games1++;
    } while (games1 < 10000);

    cout << "Out of 10,000 games1, the contestant won " << stayWins1 << " times by staying with his/her original choice and won " << switchWins1 << " times by switching his/her choice.\n";

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output:

Out of 10,000 games1, the contestant won 2462 times by staying with his/her original choice and won 2504 times by switching his/her choice.

Implementation in Python

import random
def run_trial(switch_doors, ndoors=3):
    # Pick a random door out of the ndoors available
    chosen_door = random.randint(1, ndoors)
    if switch_doors:
        # Reveal a goat
        revealed_door = 3 if chosen_door==2 else 2
        # Make the switch by choosing any other door than the initially-
        # selected one and the one just opened to reveal a goat. 
        available_doors = [dnum for dnum in range(1,ndoors+1)
                                if dnum not in (chosen_door, revealed_door)]
        chosen_door = random.choice(available_doors)

    # You win if you picked door number 1
    return chosen_door == 1

def run_trials(ntrials, switch_doors, ndoors=3):
    nwins = 0
    for i in range(ntrials):
        if run_trial(switch_doors, ndoors):
            nwins += 1
    return nwins

ndoors, ntrials = 3, 10000
nwins_without_switch = run_trials(ntrials, False, ndoors)
nwins_with_switch = run_trials(ntrials, True, ndoors)

print('Monty Hall Problem with {} doors'.format(ndoors))
print('Proportion of wins without switching: {:.4f}'
            .format(nwins_without_switch/ntrials))
print('Proportion of wins with switching: {:.4f}'
            .format(nwins_with_switch/ntrials))

You can also try this code with Online Python Compiler

Run Code

Output:

Monty Hall Problem with 3 doors
Proportion of wins without switching: 0.3290
Proportion of wins with switching: 0.6672