Introduction
We'll look at how to find the Multi Source Shortest Path in an Unweighted Graph in this blog. Getting a firm grasp on graph-based algorithms and their applications is a critical problem that has been raised in numerous interviews.

Prerequisites
Knowledge of graphs and related terminologies such as recursion, stacks, queues, trees, and the two main algorithms DFS Algorithm, BFS, and topological sorting are common prerequisites for every graph problem. It is not advisable to proceed to the shortest path issues in graphs without mastering these fundamental methods and data structures.
Nonetheless, we'll try to go through every detail needed to discover the Multi Source Shortest Path in an Unweighted Graph.
Also check Application of graph data structure
Problem Statement
What do we mean by the Multi Source Shortest Path in an unweighted graph?
Let G = (V, E) be an unweighted graph with E edges and V vertices. There are S vertices, and we have to find the distance of each vertex from one of the nearest S vertices.
Let's look at an example first.
Example
Given an Unweighted Graph G
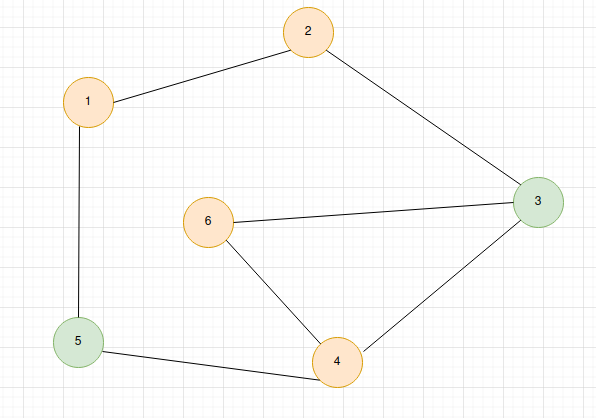
Input :
Number of Vertices = 6
Number of Edges = 9
Sources: 3, 5
Edges:
1 2
1 5
2 3
3 4
3 6
4 5
4 6Output :
Multi Source Shortest Path in Unweighted Graph
1 1
2 1
3 0
4 1
5 0
6 1Brute Force Approach
To find the closest source, we can loop through the vertices and perform a BFS (Breadth-First Search) from each vertex.
Pseudocode
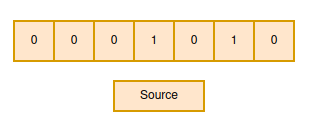
- Initialize an array source that will be 1 at an index that is the source vertex; otherwise, 0.
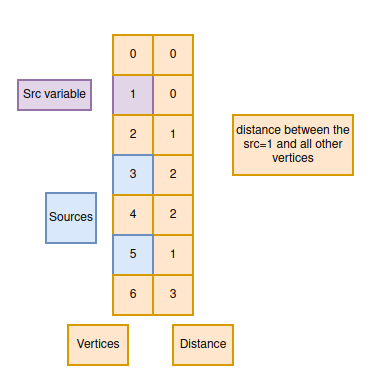
- We will run a loop to all the vertices, call BFS for each vertex, and pass it as an src variable.
- The BFS function then will find the distance between the src variables and all other vertices and store it in an array dist.
- At last, we run a loop, find the shortest distance between the src variable and multiple sources, and print it.
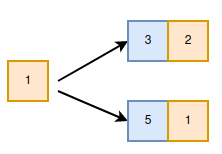
- Then repeat the same procedure.
Implementation (C++ Code)
#include <bits/stdc++.h>
using namespace std;
// The BFS function
void BFS(vector<int> adj[],int n, int src,int source[])
{
int dist[n];
for(int i = 0;i<n;i++) dist[i] = INT_MAX;
queue<int> q;
dist[src] = 0;
q.push(src);
while(q.empty()==false)
{
int node = q.front();
q.pop();
for(auto it:adj[node]){
if(dist[node] + 1 < dist[it]){
dist[it]=dist[node]+1;
q.push(it);
}
}
}
int m=INT_MAX;
for(int i = 0;i<n;i++){
if(source[i]){
m = min(dist[i],m);
}
}
cout<< src<<" "<<m<<endl;
}
// This function calculates the distance of each
// vertex from nearest source
void Multi_source_shortest_path(vector<int> graph[], int n,
int sources[], int S){
int source[n];
// reseting the source hash array
for (int i = 1; i <= n; i++)
source[i] = 0;
for (int i = 0; i <= S - 1; i++)
source[sources[i]] = 1;
// loop through all the vertices and run
// a BFS from each vertex to find the distance
// to nearest town from it
for (int i = 1; i <= n; i++) {
BFS(graph, n,i,source);
}
}
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// Driver Code
int main()
{ // Number of vertices
int n = 6;
vector<int> adj[n + 1];
// Edges
addEdge(adj, 1, 2);
addEdge(adj, 1, 5);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
addEdge(adj, 3, 6);
addEdge(adj, 4, 5);
addEdge(adj, 4, 6);
// Sources
int sources[] = { 3, 5 };
int S = sizeof(sources) / sizeof(sources[0]);
cout<<" Multi Source Shortest Path in Unweighted Graph "<<endl;
Multi_source_shortest_path(adj, n, sources, S)
return 0;
}
Output
Multi Source Shortest Path in Unweighted Graph
1 1
2 1
3 0
4 1
5 0
6 1Complexity Analysis
Time Complexity: O(V.(V+E))
We run a loop through the vertices, and from each vertex, run a BFS to find the closest source vertex. This will take O(V.E).
Space Complexity: O(V)
We are using a dist array to store the distance of each vertex from its nearest source and a queue whose space is the same as the number of vertices.
Read More - Time Complexity of Sorting Algorithms





