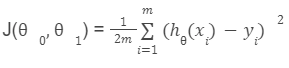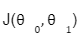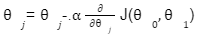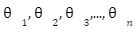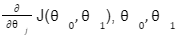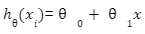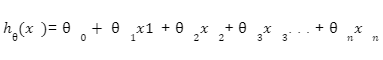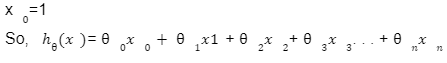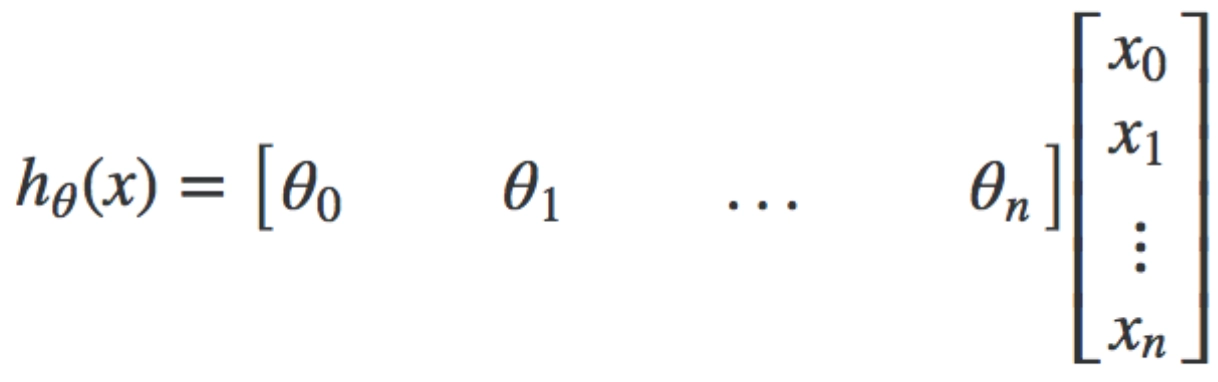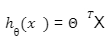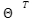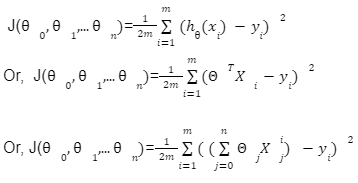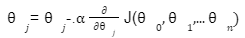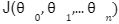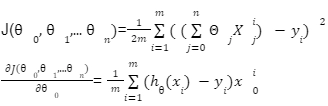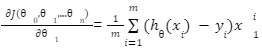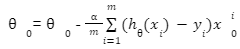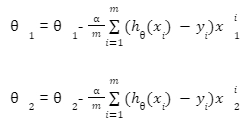Introduction
In simple words, Regression is the process of estimating the relationship between the dependent and independent variables.
Linear Regression is a technique to describe a linear function that fits a best-suited line to the data points. Best suitable means the sum squared error for each data point to the bar is minimum.
A few examples of the Regression problem can be the following
1. "What is the market value of the house?"
2. "Stock price prediction."
3. "Sales of a shop."
4. "Predicting the height of a person."
We will use the following terms in our discussion:
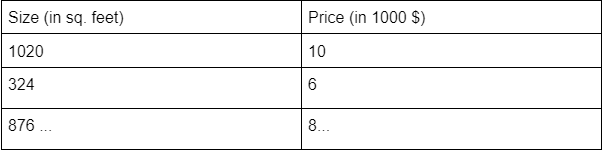
1) Features
Features are simply the independent variables plotted on the x-axis.
E.g., for house data, the features are the size of the house, no. of bedrooms, no. of kitchens, etc.
2) Target: The target variable is the output or dependent variable whose value depends on the independent variable.
E.g., for house data, the pricing of a house is the target variable whose value is dependent on the features of the house.
3) Hypothesis function: The hypothesis function is the function that fits a linear model to the data points. It is the general equation of a line given as:
Y=m1X1+m2X2+m2X3+...+mnXn+C
Y is the dependent/target variable.
M1,m2,m3...mn are the slope parameters of the line in multiple dimensions.
X1, X2, X3…, Xn are the features or independent variables.
C is the Y-intercept of the linear Regression line.
If we restrict ourselves to only one independent variable, the equation will look like Y=mx+C.
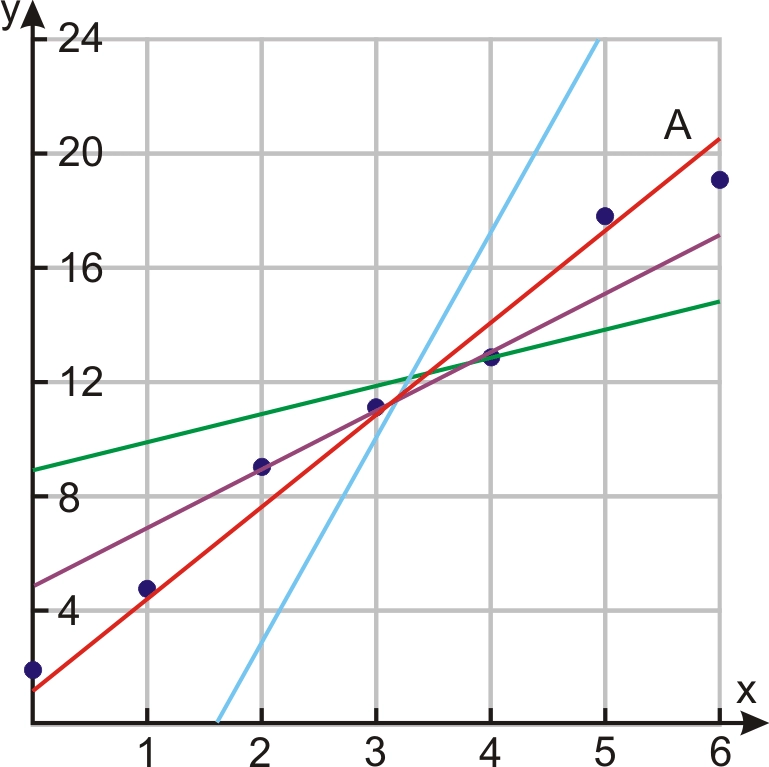
Source: ck12.org
The value of Y gives us the predicted value of the given input variable. There could be multiple lines that seem to fit our data. But, we have to select the best fit line out of all. In other words, the magnitude of the sum of squared differences between the actual and predicted values should be minimum.
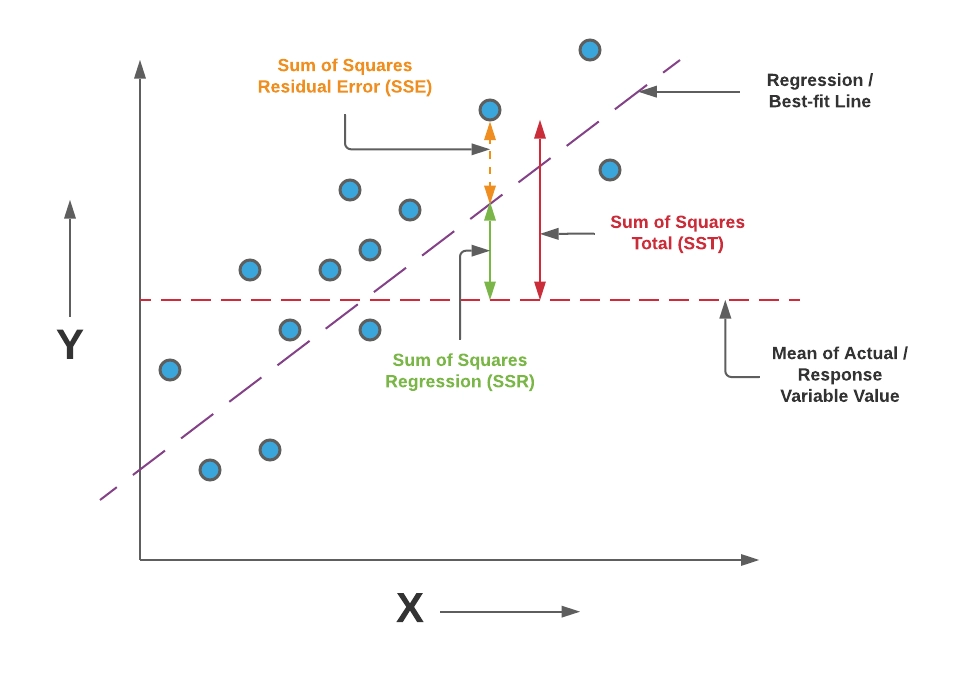
Source: vitalflux.com
If yi is the actual output and,
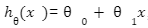 , is the output predicted by the Regression line
, is the output predicted by the Regression line
Then squared sum error is = 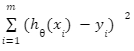 .
.
Where m is the number of datasets.
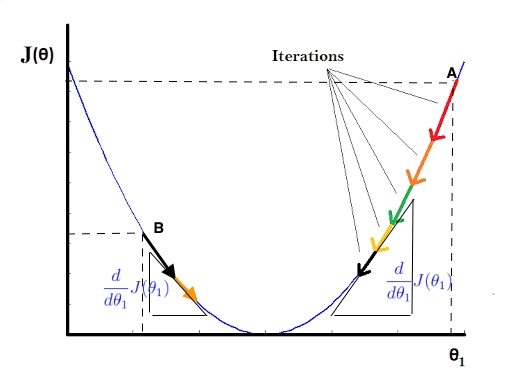
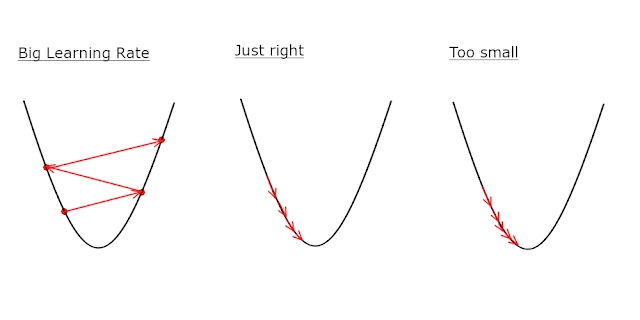
We can check the accuracy of our hypothesis function by using the cost function:
Cost function
The goal is to find the minima the above cost function
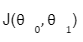
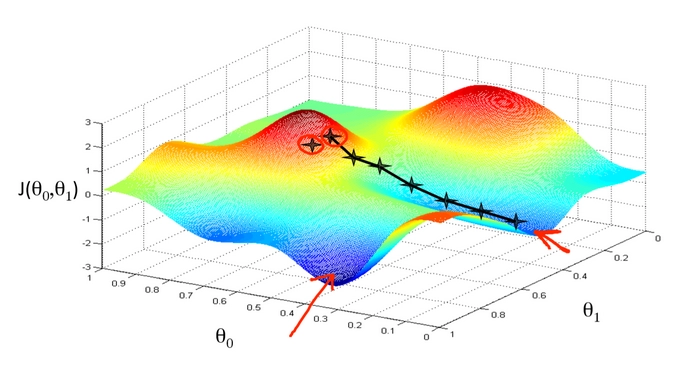
The plot of our cost function would like:
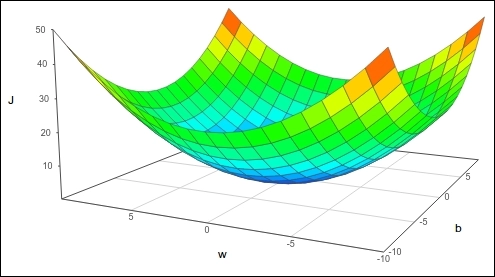
Source: concise.org
The plot will look like a 3-D parabola. We won't be dealing with 3-D parabola; instead, we will be dealing with "Contour plots."
A contour plot is a graphical technique to represent a 3-D model in the 2-D plane by plotting z slices.
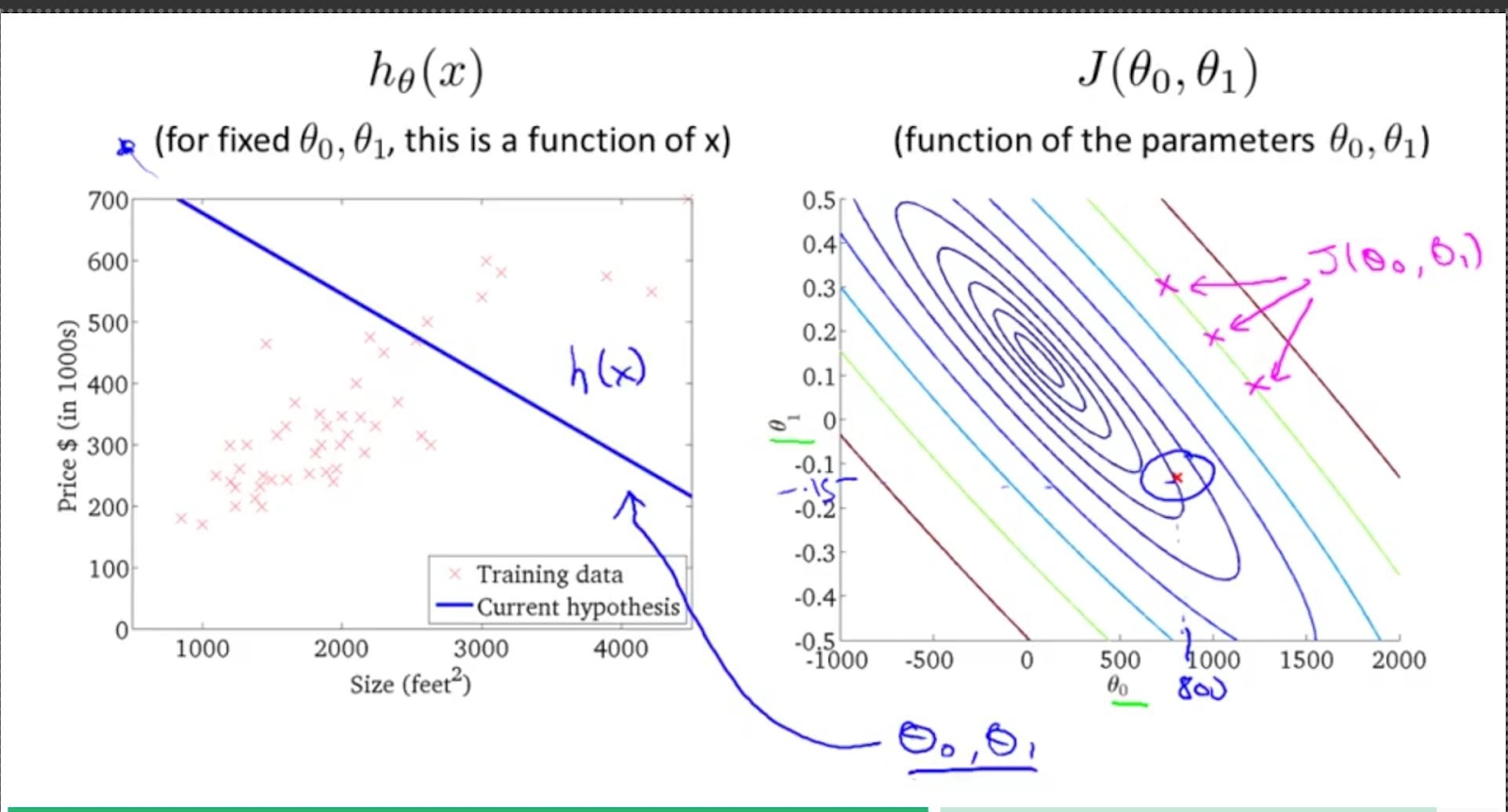
All three points x1,x2,x3 drawn in magenta have the same value for
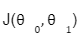 .
.