N-ary Heap

Introduction

Before beginning, let's recap what a complete binary tree and binary heap are. 

A complete binary tree is a tree in which each node can have a max of two children, and all the levels should be completely filled except for the last level, where nodes should be filled from left to right. For example tree in the first image is not a complete binary tree.

For a detailed understanding of heaps, check out Understanding Heap Data Structure
 

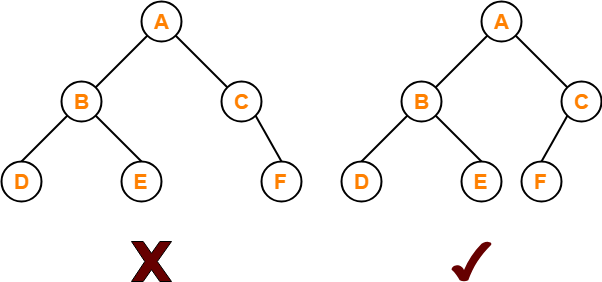
A binary Heap is a complete binary tree where nodes are in a specific order depending upon whether it is a max heap or a min-heap.
You can go through this article to learn more about the binary heap data structure.

N-ary heaps are similar to binary heaps. They are a generalized version of binary heaps. Unlike binary heap, n-ary trees can have a maximum of n children instead of 2. N-ary heaps have the following properties: 

1. It is a complete n-ary tree where all the levels are filled except for the last level,  where nodes are filled from left to right.
2. N-ary heaps are of 2 types: 
   1. Min N-ary Heap: The value at each node should be smaller than its children. 

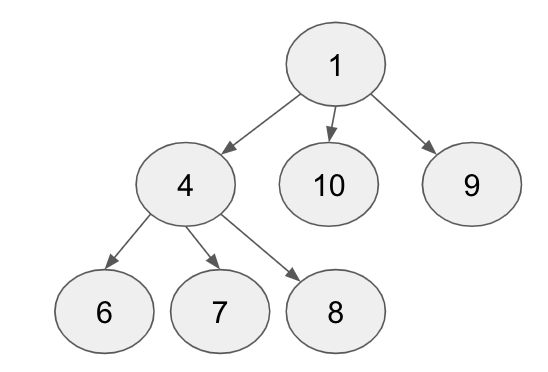
1. Max N-ary Heap: The value at each node should be greater than its children.    

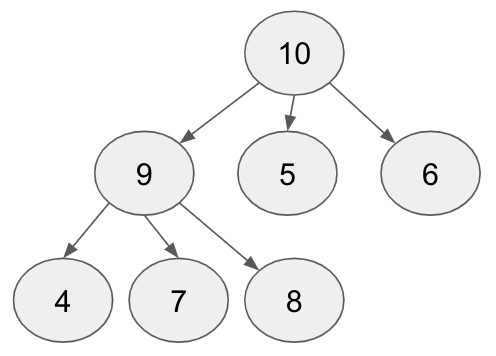
Implementation (Max Heap)

We will store the n-ary heap in the form of an array where: 

1. The maximum value node will be at the 0th index.
2. The parent of a node at the ith index will be at (i-1)/k.
3. The children of a node at the ith index will be at indices: (k*i)+1, (k*i)+2 … (k*i)+k.
    

getMax(): It returns the maximum element in the heap

isEmpty(): It returns true if the heap is empty.

Insert(): It inserts a new element in a heap. The operation to insert an element in an n-ary heap is similar to inserting a value in a binary heap. First, insert the element at the end of the tree. Then heapify upwards, i.e., traverse until the parent is smaller than the element inserted.

removeMax(): To delete the max key, we replace the key at the 0th index with the last element and pop out the last element. Then we will heapify downward until we reach a stage where all the node's children are smaller than the parent node.

Code in C++

#include<iostream>
#include<climits>
#include<vector>
using namespace std;

// implementation of n-ary max heap
class n_ary_heap{
	int n;
public:
	vector<int> pq;
	// constructors
    n_ary_heap(){
        n = 2; // by default - binary heap
    }
    n_ary_heap(int k){
        n = k;
    }

    // get the maximum value from the heap
    int getMax() {
        if(pq.size()==0){
            // no element
            return INT_MIN;
        }
        return pq[0];
    }

    bool isEmpty() {
        if(pq.size()==0){
            return true;
        }else{
            return false;
        }
    }

    // inserting a value in the heap
    void insert(int value) {
        // first insert it at the bottom
        pq.push_back(value);
        
        // Now heapify up till we place the value at the correct position
        int childrenIndex = pq.size()-1;
        int parentIndex = (childrenIndex-1)/n;
        while(parentIndex>=0 && pq[childrenIndex]>pq[parentIndex]){
            // since the value at the childrenIndex is greater and it is max heap, so we should swap
            swap(pq[childrenIndex],pq[parentIndex]);
            
            childrenIndex = parentIndex;
            parentIndex = (childrenIndex-1)/n;
        }
    }

    // removing the maximum element from the heap - which will be at the top in case of a max heap
    void removeMax() {
        pq[0] = pq[pq.size()-1];
        pq.pop_back();
        
        int parentIndex = 0;
      
        while(1){
            int largestValueIndex = parentIndex;
            
            // visit all its children and find the maximum value child among them
            for(int i=n*parentIndex+1; i<=(n*parentIndex + n) && i<pq.size();i++){
                if(pq[largestValueIndex]<pq[i]){
                    largestValueIndex = i;
                }
            }
            
            if(largestValueIndex==parentIndex){
                break;
            }else{
                // if the largest index is not the parent index, we need to heapify down
                swap(pq[parentIndex],pq[largestValueIndex]);
                parentIndex = largestValueIndex;
            }
        }
    }
};


int main(){
	n_ary_heap max_heap(3);

	vector<int> arr{4, 5, 6, 7, 8, 9, 10};

	// insert all the elements in the n-ary heap one by one
	for(int i=0;i<arr.size();i++){
		max_heap.insert(arr[i]);
	}

	// 	    Heap after inserting all the elements
	//        10
	//       / | \
	//      9  5  6
	//    / | \
	//   4  7  8

	cout<<"The maximum Element in the heap is: "<<max_heap.getMax()<<endl;

	max_heap.removeMax();
	cout<<"The Maximum Element after removing the previous max in the heap is: "<<max_heap.getMax()<<endl;

	// 	    Heap after removing the max element
	//         9
	//       / | \
	//      8  5  6
	//    / | 
	//   4  7  
} 

You can also try this code with Online C++ Compiler

Run Code

Output

The maximum Element in the heap is: 10
The Maximum Element after removing the previous max in the heap is: 9

Complexity Analysis

Time Complexity

Since for a k-ary heap, the maximum height of the heap will be log_kn, where n is the number of elements in a heap. 

1. For insertion, we do heapify upwards, and since the maximum height of the heap can be log_kn, the time complexity for inserting a value in a heap is O(log_kn), where n = number of elements in the heap.
2. Time Complexity for fetching the maximum element is O(1).
3. For removing the max element, we do downward heapification, and since the maximum height of the heap can be log_kn. At each level, we compare all the k children of the node with the parent, the time complexity for removing the max element from the heap is O(k*log_kn) where n = number of elements in the heap.

Space Complexity

Since we are maintaining an array to store the elements of the heap, space complexity is O(n), where n = the total number of elements in the heap.

Check out this problem - Largest BST In Binary Tree

Also Read, Prefix Sum Array