Introduction
The Noisy Channel model is related to language modelling. So what is the noisy channel model, and why is it so important in natural language processing?
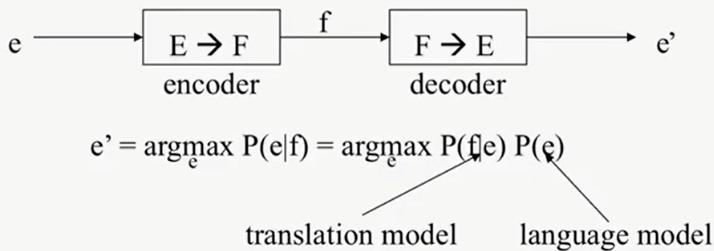
So let's take a hypothetical system that takes an input written in English. Let's call it X, and then we have some encoder that randomly misinterprets the information, converting it to Y, which is some garbled English. So the output will be what we call spoken English or Y. The garbling is just converting the original English words into an audio signal corresponding to spoken English. Let us look at more examples. We can convert grammatical English X to English with grammatical mistakes Y. We can convert English X to bitmaps or characters Y. In a more general case, the noisy channel model determines the connection between a joint probability of two sequences as the product of the first sequence times the likelihood of the second one given the first one. We can think of it as a process of encoding and decoding. So given our foreign language string, we want to guess the English version. We assume that 'e' was converted to 'f' using an encoder. Then, we want to build a decoder that converts 'f' into 'e.' Here, I am using this notation e’ (with an apostrophe) to indicate that this is our estimate, which doesn't mean that it's the original. It's just our best guess as to what ‘e’ is.
So how do we determine e.? Well, ‘e’ will be the value that maximises the conditional probability of the English sentence given the following sentence. So, according to the Bayesian formula, we can write the expression that maximises the product of the conditional probability f given e times the probability of ‘e’.
P (f|e) Is a noisy channel model known as a translation model, and P(e) is the language model. A language model takes a sequence of words in a given language, and it tells us how likely it is that a particular series is a valid sentence.
Now, I will introduce the translation model, which essentially tells us that given a particular sentence in English, what's the probability that this specific sentence in the foreign language corresponds to the ruling in English.
So let's take an example from French that translates "la Maison Blanche" Into English. So here are some possible translations. The first one that we're going to solve is "cat plays the piano." The probability that this foreign string "la Maison Blanche" matches the English line "cat plays the piano" is very low, so we will put the minus in that box. What about the English language probability of a "cat plays piano.?" Again, this is not a proper sentence, so we will give it a low score. The next one is a little bit better. We have the possible translation as "House White the ."This is not a grammatical sentence, but it matches the right words in French. So we will give it a positive score for the translation model and a negative score for the language model. Next, there is a little bit better "the House White," again, this is not a grammatical sentence in English but matches the French words. So we will give it the same set of scores as that of the previous example.
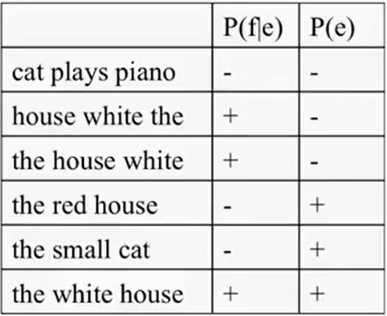
Similarly, as shown here in the table, we can assign the scores to the rest of the sentences.
The idea of the translation model is to come up with all the possible sequences of words in English of the right length to try to figure out, based on the two probabilities in the two columns, which one is the best translation of the original sentence. So a good translation will have a high score on their language model and a high score on the translation model. If many phrases have high scores on both of the columns, we're just going to multiply those two probabilities and pick the one with the highest product.
Use Cases
Handwriting recognition- The input will be the bitmap, and the output will be an English sentence.
Text generation
Text summarization
Machine translation
Spelling correction- In spelling correction, we can use it to model the probability that a specific type of mistake will be made.




