Non-overlapping sum of two sets

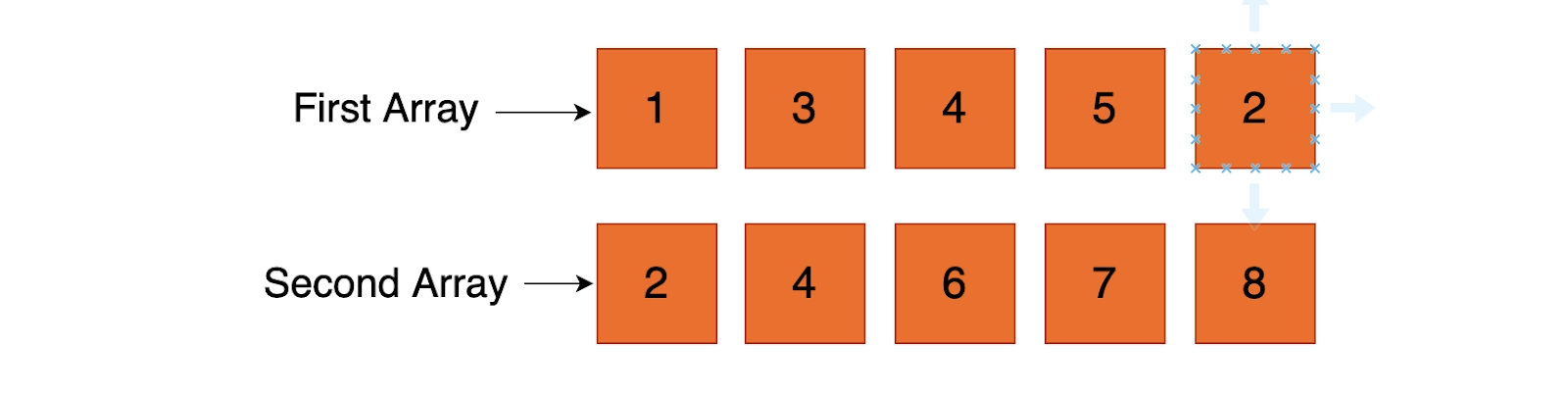
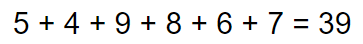Approach I (Brute Force)

One straightforward method is; For each element in A[] that is not present in B[], add that element to a variable (let’s call it as sum). In the same manner, traverse B[] and do the same.

Algorithm

Let’s quickly walk through the algorithm for the Non-overlapping sum of two sets problem:

1. Create two variables: a boolean flag and an integer sum
    
2. while i < size, traverse the array
   
   
   • while j < size, traverse the second array
     
     
     • If the i’th element is not present in the second array
       
       
       • Add i’th element to the sum
          
3. Repeat for the second array
    
4. Print Sum

Time Complexity 

O(N2) Where ‘N’ stands for the length of the array as provided in the problem statement of the Non-overlapping sum of two sets.

Reason: For each element in the A array, we are traversing another array of size N.

Auxiliary Space Complexity 

O(1) Where ‘N’ stands for the length of the array as provided in the problem statement of the Non-overlapping sum of two sets.

Reason: We are only traversing throughout the program. We don’t need auxiliary space.

You can also read about the Longest Consecutive Sequence.

Approach II (Hashing)

Two input arrays with some of the elements shared between them have been provided, as per the problem (Non-overlapping sum of two sets) statement. Finding the entire sum of all the uncommon members in both arrays is required by the statement. Hashing will be utilized for this. A hashmap uses keys and values; each key in the hashmap has a corresponding value. Consequently, everything functions as a whole. We'll declare a hashmap and put the elements from both arrays into it in a single map together with their frequencies.

Algorithm

Let’s quickly walk through the algorithm for the Non-overlapping sum of two sets problem:

1. Create a map.
    
2. while i < n, traverse the array
   
   
   • Both of the array's elements' frequencies are counted and entered into the map.
      
3. Set total as 0
    
4. Iterate the map.
   
   
   • Verify that the map has an element with a value of 1.
      
   • If so, continue to add each element to the total.
      
5. Return the computed total.

Algorithm Walkthrough

• After creating a map, we’ll iterate through the first array counting occurrence of each element, as shown below:

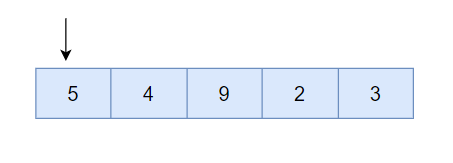
• Map after traversing the first array,

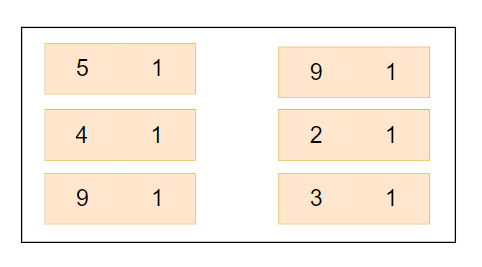
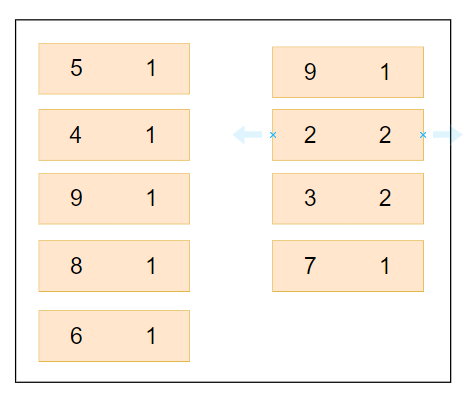
• Now, traversing the second array, counting the occurrences of each element in the same map;

• Map after traversing the second array,

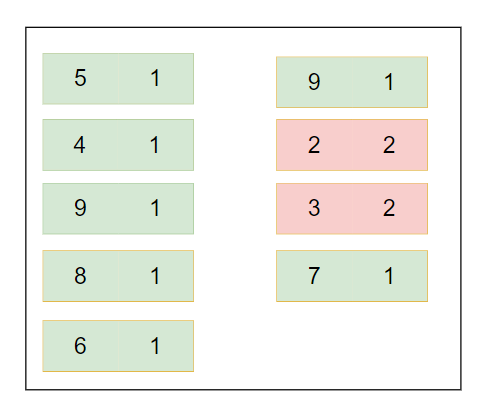
• At last, we need to iterate through the map, and count elements that occurred only once, here green are valid ones.

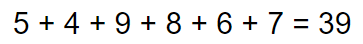
Implementation in C++

C++ program to find Non-overlapping sum of two sets.

#include <bits/stdc++.h>
using namespace std;

/* calculation function for the non-overlapping sum of two arrays */
int totalSum(int FirstArray[], int SecondArray[], int size) {
	unordered_map<int, int> hash;
	for (int i = 0; i < size; i++) {
		hash[FirstArray[i]]++;
		hash[SecondArray[i]]++;
	}
	/* determine the non-overlapping sum */
	int total = 0;
	
	for (auto i: hash)
	if (i.second == 1)
		total += i.first;
	return total;
}

int main() {
	int FirstArray[] = { 5, 4, 9, 2, 3 };
	int SecondArray[] = { 2, 8, 7, 6, 3 };
	int n = sizeof(FirstArray) / sizeof(FirstArray[0]);
	cout << totalSum(FirstArray,SecondArray, n);
	return 0;
}

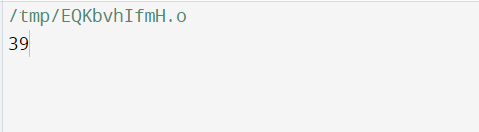
Output

Implementation in Java

Java program to find Non-overlapping sum of two sets

import java.io.*;
import java.util.*;

class HelloWorld {
	/* calculation function for the non-overlapping sum of two arrays */
	static int findSum(int[] FirstArray, int[] SecondArray, int size) {
		// Element inserting
		HashMap<Integer, Integer> hash = new HashMap<>();
		for (int i = 0; i < size; i++) {
			if (hash.containsKey(FirstArray[i]))
				hash.put(FirstArray[i], 1 + hash.get(FirstArray[i]));
			else
				hash.put(FirstArray[i], 1);
			if (hash.containsKey(SecondArray[i]))
				hash.put(SecondArray[i], 1 + hash.get(SecondArray[i]));
			else
				hash.put(SecondArray[i], 1);
		}

		/* determining the non-overlapping sum */
		int total = 0;
		for (Map.Entry entry : hash.entrySet()) {
			if (Integer.parseInt((entry.getValue()).toString()) == 1)
				total += Integer.parseInt((entry.getKey()).toString());
		}

		return total;
	}

	public static void main(String args[]) {
		int[] FirstArray = { 5, 4, 9, 2, 3 };
		int[] SecondArray = { 2, 8, 7, 6, 3 };
		int n = FirstArray.length;
		System.out.println(findSum(FirstArray, SecondArray, n));
	}
}

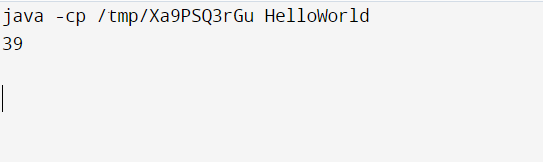
Output

Implementation in Python

Python program to find Non-overlapping sum of two sets.

from collections import defaultdict

# Calculation function sum of two array without overlap
def findSum(first, second, n):
    # element insertion
    hash = defaultdict(lambda:0)
    for i in range(0, n):
        hash[first[i]] += 1
        hash[second[i]] += 1
    # sum calculation
    total = 0
    for x in hash:
        if hash[x] == 1:
            total += x
    return total
 
if __name__ == "__main__":
    first = [5, 4, 9, 2, 3]
    second = [2, 8, 7, 6, 3]
    # array size
    n = len(first)
    # calling function
    print(findSum(first, second, n))

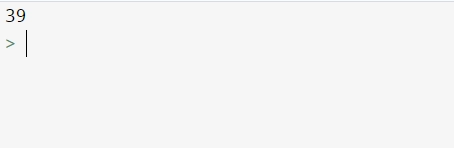
Output

Time Complexity 

O(N) Where ‘N’ stands for the length of the array as provided in the problem statement of the Non-overlapping sum of two sets.

Reason: O(n), where "n" is the array's length. All of the operations for finding, deleting, and updating are completed in O(1) time complexity because we utilized a hashmap. As a result, linear time complexity was accomplished.

Auxiliary Space Complexity 

O(N), Where ‘N’ stands for the length of the array as provided in the problem statement of the Non-overlapping sum of two sets.

Reason: The elements of both arrays must fit somewhere on the map.

Frequently Asked Questions

Explain what is hashing?

Any key or string of characters can be transformed into another value by hashing. The original string is typically represented with a shorter, fixed-length value or key that makes it simpler to locate or use.

What does a data structure's hash key mean?

A form of data structure that contains key-value pairs is a hash table. A hash function receives the key and runs mathematical operations on it.

What is the DP problem?

Dynamic programming, often known as DP, is an algorithmic technique for solving problems by recursively dividing them into easier subproblems and taking advantage of the fact that the best solution to the whole problem depends on the best solution to each of its individual subproblems.

Why is hashing necessary?

When compared to alternative data structures, hashing offers a more flexible and secure way to retrieve data.

Why is hashing quicker?

The linear time complexity of O(n) is presented when searching through an array-like data structure. In other words, the search time grows linearly in proportion to the size of the data structure.

Conclusion

This article has gone through problems related to Hashing, we have discussed the question: Non-overlapping sum of two sets in multiple languages. To master the topic, check out some of our resources about hashmap, HashMap Implementation, and Introduction to HashMap.

Refer to our guided paths on Coding Ninjas Studio to learn more about DSA, Competitive Programming, JavaScript, System Design, etc. Enroll in our courses and refer to the mock test and problems available. Take a look at the interview experiences and interview bundle for placement preparations. Check out our articles in Library. You can now easily attempt the sum of two arrays problem.
Do upvote our blog to help other ninjas grow.
Happy Learning!