Number of Binary Search Trees of Height H Consisting of H+1 Nodes

Approach

Every BST with a height of ‘H’ and containing only ‘H+1’ nodes will be a skew binary search tree. And in a skew BST, at each node, we can either choose the greatest value or the smallest value from the given set of nodes.

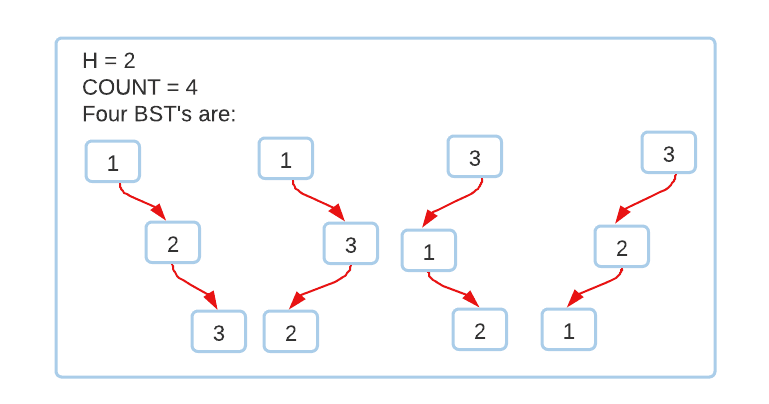
Example

So for each ‘H’ node value in the BST, we choose from two values, either the greatest or the smallest, except for the last ‘H + 1th node, where we’ll have only one choice.

So the number of BST’s with height ‘H’ and nodes value from 1 to ‘H + 1 are 2 * 2 * . . 2 (H times) = 2 ^ H. .

Now that we know we just have to calculate 2^H, let’s see how the algorithm works.

1. Initialize two integers X = 2 and COUNT = 1.
2. Next, we loop until ‘H’ is not zero.
   1. If ‘H’ is odd, multiply ‘X’ with ‘COUNT.’
   2. Next, divide ‘H’ by two.
   3. And update ‘X’ to ‘X * X.’ {Since A ^ B = (A * A) ^ (B /2), where B is even.}
3. Return ‘COUNT’.

Program

#include <iostream>
using namespace std;

const int modulo = 1000000007;
typedef long long ll;

// Function counts the number of Binary Search Trees of height H consisting of H + 1 nodes.
int countNumberOfBST(int h)
{
   // Initialize x=2.
   ll x = 2;
   
   // 'COUNT' that will store 2^'H'.
   int count = 1;
   
   // Loop until 'H' is not zero.
   while (h > 0)
   {
       // If 'H' is odd, multiply 'COUNT' with 'X.’
       if (h & 1)
       {
           count = (count * x) % modulo;
       }
       
       // Now divide 'H' by two.
       h = h >> 1;
       
       // Update 'X' to 'X'^2.
       x = (x * x) % modulo;
   }
   
   // Return the 'COUNT'.
   return count;
}

int main()
{
   int h;
   cout << "Enter the value of H: ";
   cin >> h;
   int count = countNumberOfBST(h);
   cout << "The Number of Binary Search Trees of height H consisting of H + 1 nodes: " << count << endl;
   return 0;
}

Input

Enter the value of H: 4

Output

The Number of Binary Search Trees of height H consisting of H + 1 nodes: 16 

Time Complexity

O(log(H)), where ‘H’ is the given height.

Since we divide ‘H’ by two, every time in the loop until it’s zero, the time complexity is O(log(H)).

Space Complexity

O(1)

As we are not using any additional space.

You can also read about insertion into bst.

Frequently Asked Questions

What is a Binary Tree?

A Binary Tree is a generic tree with every node having at most two children. A node can have any number of children in generic trees, but in binary trees, a node can only have a left and a right child.

What are Binary Search Trees?

A Binary Search Tree is a Binary Tree where the value of every node of the tree is larger than the maximum value of its left subtree and lesser than the minimum value of its right subtree.

Why are Binary Search Trees used?

In Binary Search Trees, the searching becomes very fast compared to the Binary Trees because, at each node, we can judge if we should go to left subtree or right subtree (i.e., if the key value is lesser than the node value, then we’ll go to left subtree to search our key node & if the key value is greater than the node value we’ll proceed to right subtree to search our key node).
The time complexity to search an element is O(log2n), where n is the number of nodes in the binary search tree.

Conclusion

A fascinating follow-up problem for the above problem would be to build these 2 ^ H trees. On the Coding Ninjas Platform, we have various such problems and blogs. Additionally, Coding Ninjas recently introduced the Coding Ninjas Studio Test Series, a test series developed for acing tech interviews.

Recommended Reading:

• Lowest Common Ancestor of Binary Tree
• Minimum Height of the Binary Search Tree Created From the Given Array
• Traverse a BST in a Min-Max Manner
• Find the Closest Value For Every Element in the Array
• Sum of All Nodes With Smaller Values at a Distance K From a Given Node in BST
• Reverse a Path Using Queue in BST
• Number of BSTs

Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.

Thanks for reading. I hope you’ve gained a lot from this blog.