Introduction
Here in this blog, we are asked to see various approaches to find the number of binary trees for a given preorder sequence length. We already are familiar with the concept of binary trees and graph traversals like preorder, postorder, and postorder. In preorder, we traverse the root node first, then the left node and right node. While in postorder, we traverse the left node first, then the right node, and in the last, we traverse the root node. And if we talk about inorder traversal, we traverse the left node first, then the root node, and in the end right node. So, let's see the approach in detail.

Source: binary tree
Problem Statement
In this problem, we are given a preorder sequence length. And from that, we need to find the number of binary trees we can make. We can try different approaches to solve this problem. There are three traversal techniques available which are: preorder, postorder and inorder. Here we need to use preorder sequence length to get the desired result. Let us understand the problem statement with the help of an example.
Must Recommended Topic, Binary Tree Postorder Traversal.
Sample Example
Let us understand this problem statement with the example given below.
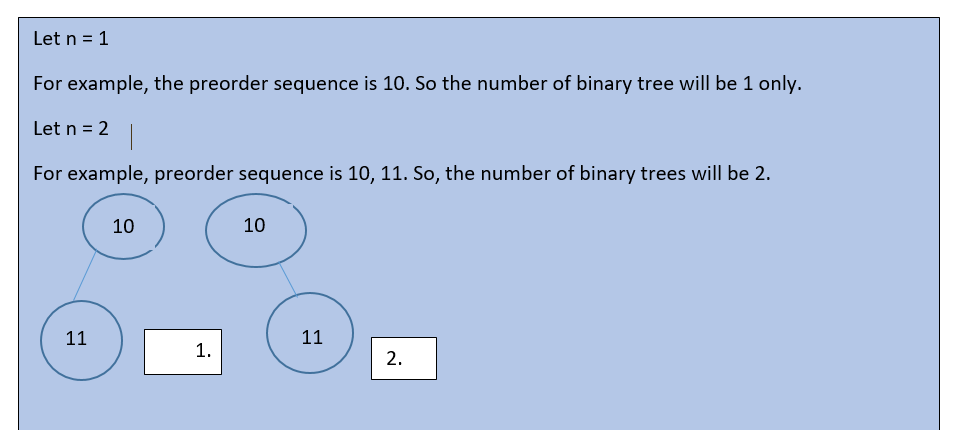
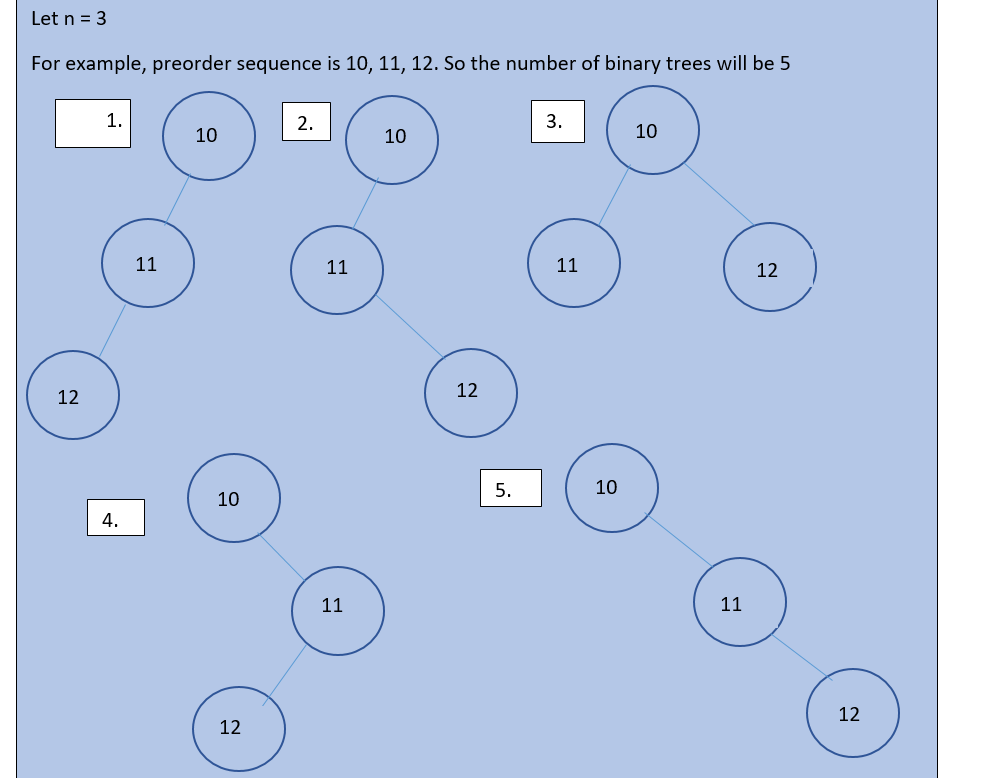


From the above diagram, it is clear how we have to proceed with the problem statement. We got that how from the given sequence of preorder traversal we can calculate the number of binary trees. And what does the problem statement says? In the same way, we can create the number of binary trees possible for n = 5 and so on. Now let us see the approach to solve this problem.
Dynamic Programming Approach
Dynamic programming is an optimization approach. We can use Dynamic Programming to optimize any recursive solution that has repeated calls for the same inputs. The idea is to simply save the results of subproblems so that we don't have to recalculate them later. This straightforward optimization reduces the time complexity from exponential to polynomial.

Source: dynamic programming
Let us see its algorithm to understand how dynamic programming is used here.
Steps of Algorithm
Step 1: We will create an array to store the number of binary trees formed.
Step 2: Then we will initialize:
BinaryTree[i] = 0
BinaryTree[0] = BinaryTree[1] = 1
Step 3: We already are aware that for preorder 1 node there will be only one binary tree. So we will start the loop from n = 2, i.e. i=2 and the inner loop j will run from 0.
for (int i = 2 to i <= n and increment i)
for (int j = 0 to j < i and increment j)
BinaryTree[i] += BinaryTree[j] * BinaryTree[i - j - 1];
Step 4: Then for any value of n given, we will call the function and print the value of BinaryTree[n].
Let us see the implementation of this approach in the next section of this blog.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
int CountBinaryTrees(int n)
{
int BinaryTree[n + 1]; //for storing number of Binary trees formed
memset(BinaryTree, 0, sizeof(BinaryTree));
BinaryTree[0] = BinaryTree[1] = 1; //initializing that with 0 and 1 node there will be only one binary tree possible
for (int i = 2; i <= n; ++i) //loop will start from 2, because we are already aware for 1 node
for (int j = 0; j < i; j++)
BinaryTree[i] += BinaryTree[j] * BinaryTree[i - j - 1];
return BinaryTree[n];
}
int main()
{
int n;
cout<<"enter the sequence of preorder: "<<endl;
cin>>n;
cout << "Total Possible Binary Trees for node "<< n << " are: "<<CountBinaryTrees(n) << endl;
return 0;
}
Output:
enter the sequence of preorder:
4
Total Possible Binary Trees for node 4 are: 14
Implementation in Python
def CountBinaryTrees(n) :
BinaryTree = [0] * (n + 1) #for storing count of binary trees
BinaryTree[0] = BinaryTree[1] = 1 #initializing for 0 and 1 there will be only 1 tree possible
for i in range(2, n + 1): # we will start the loop from 2
for j in range(i):
BinaryTree[i] += BinaryTree[j] * BinaryTree[i - j - 1]
return BinaryTree[n]
if __name__ == '__main__':
n = int(input("Enter the sequence of preorder: "))
print("Total Possible Binary Trees for node ",n," are:",CountBinaryTrees(n))
Output:
Enter the sequence of preorder: 4
Total Possible Binary Trees for node 4 are: 14
Now let us analyze the time and complexity of the above approach.
Complexity analysis
Time complexity
The time complexity of this algorithm is O(n^2) where n is the number of elements. The time complexity appears to be increased as a result of two loops that we are using in the code. The first loop i runs from 2 to i <= n and the second loop j runs from 0 to i. So overall it will take n^2 time. So the complexity will be O(n^2).
Space complexity
If we consider the space used to store the result then the space complexity is O(n) otherwise we can consider the space complexity to be O(1).
Check out this problem - Count Ways To Reach The Nth Stair




