Introduction
This blog will discuss the solution to the problem to find the number of pairs with a given sum in a binary search tree. Before we deep dive into the solution of this problem, we should look at some examples to have a better understanding of this problem.
Sample Examples
Input: X = 15

Output: Total number of pairs: 1
The possible pairs are: {7, 8}
Input: X = 7
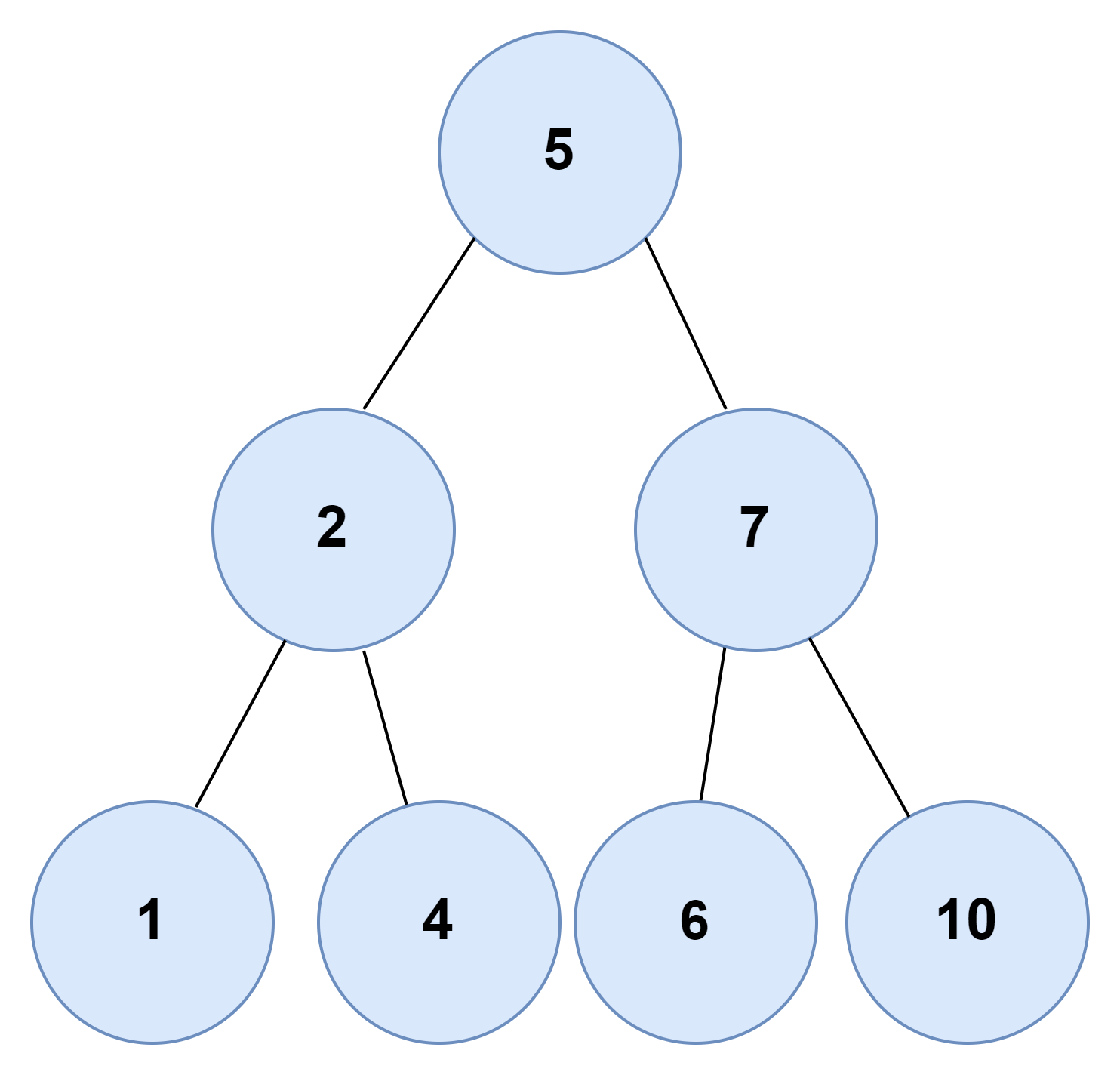
Output: Total number of pairs: 2
The possible pairs are: {{2, 5}, {1, 6}}
Brute Force Approach
The brute force approach of this problem to find the number of pairs with a given sum in a binary search tree is to hash all the node values of the bst in the map. Then we will find pair by checking the map. For example, consider the value of given sum as x and suppose two nodes have values as a and b are present in the bst; since we have hashed all the node values of the bst beforehand, we will iterate in the map. When we find a, we will first check if it is less than x or not. If it is, then we will add m[X-a] into our answer, and we will now change the value of both m[a] and m[b] to zero. We will repeat this process till we reach the end of the map.
Algorithm
- We will make a function inorder() which will take one argument, i.e., the tree's root. We will maintain a map and hash all the elements of the bst into the map while traversing the bst.
- Now in the main code, we will traverse the map and now suppose the current element of the map is a. Now we will check if a is less than x and if it is, then we will add m[X-a] to our answer, and after that, we will change the values of both m[a] and m[b] to zero.
- After the map iteration is over, we will print our answer.
Code in C++
// C++ implementation to find the number of pairs with a given sum in a binary search tree
#include <bits/stdc++.h>
using namespace std;
// Structure of each node of BST
struct Node
{
int key;
struct Node *left, *right;
};
// Function to create a new BST node
Node *TreeNode(int data)
{
Node *temp = new Node();
temp->key = data;
temp->left = temp->right = NULL;
return temp;
}
// Function to insert node in bst
struct Node *insert(struct Node *node, int key)
{
// If the tree is empty, then return a new node
if (node == NULL)
return TreeNode(key);
// Otherwise, recur down the tree
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
// Return the (unchanged) node pointer
return node;
}
// to hash the elements of the bst
map<int, int> m;
// Function to count pairs with given sum
void inorder(struct Node *root)
{
// base case
if (!root)
return;
// hashing the current node in the map
m[root->key]++;
inorder(root->left);
inorder(root->right);
}
int main()
{
/* Formation of BST 1
5
/ \
2 7
/\ /\
1 4 6 10
*/
struct Node *root1 = NULL;
root1 = insert(root1, 5);
insert(root1, 2);
insert(root1, 1);
insert(root1, 4);
insert(root1, 7);
insert(root1, 6);
insert(root1, 10);
int x = 7, ans = 0;
inorder(root1);
for (auto y : m)
{
// if x is greater than the element
if (x > y.first)
{
// we will add the hash value of (x-y.first)
ans += m[x - y.first];
m[x - y.first] = 0;
m[y.first] = 0;
}
}
cout << "The total number of pairs are:" << ans << endl;
return 0;
}
Output:
Output: Total number of pairs are: 2 Complexity Analysis
Time Complexity: O(N)
Since we are doing in order traversal of the bst and inorder traversal can be done in O(N), the time complexity is O(N).
Space Complexity: O(N)
Since we are using a map to store the frequencies of all the nodes of the bst, therefore, the space complexity is O(N).