Problem
Given an N * M grid, you have to draw K rectangles such that the current rectangle is completely inside the last-drawn rectangle, i.e., the new rectangle should not have any common point with the previous one. You have to count the number of ways to draw K rectangles. Since the answer can be large, you must print the answer modulo 10 ^ 9 + 7.
Note: Two ways to draw K rectangles are considered different if the final images are distinct.
Example -
Input
5 5 2
Output
1
Explanation
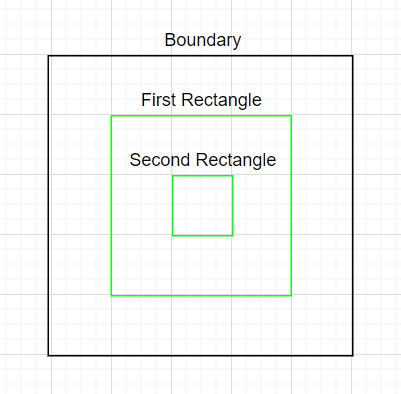
The only way to draw two rectangles inside a 5 * 5 grid such that the new rectangle is completely inside the previous rectangle is to draw the first rectangle of size 3 * 3 and the second rectangle of size 1 * 1 inside it. Therefore, the number of ways to draw K rectangles is 1.
Input
3 4 1
Output
3
Explanation
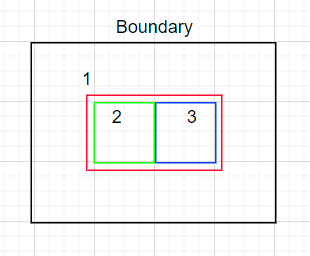
The figure above shows the three ways to draw one rectangle inside a 3 * 3 grid. We can show that there is no other way to draw one rectangle. Therefore the number of ways to draw K rectangles for this example is 3.
Also see, Euclid GCD Algorithm
Approach
Let us imagine the problem in 1-dimension by considering that we have a horizontal line of length N. Drawing a rectangle can be considered equivalent to marking two points on this line such that the next two points are completely inside the previously marked points.
For example, if N is five and we have to mark two pairs of points, the following diagram shows how the final image will look.
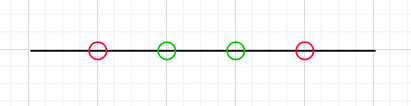
The first pair of points will be the outermost (red), and the second will be the inner points (green). This is the only way to draw two pairs of points satisfying the condition on a line of length N.
One thing to observe here is that once we fix the points, the order gets automatically fixed. The outer pair will be marked first, the second outer pair will be marked next, and so on.
Thus our problem now reduces to finding K pairs of points inside a line of length N. That is, we have to mark 2*K points on a line of length N. This can be calculated using binomial coefficients. The final formula for 1-D will be:
nCr(N-1, 2*k)
Now, to solve the problem in 2-D, we have to consider both dimensions. Since these dimensions are independent of each other, the final answer will be the multiplication of their individual answers. Thus the number of ways to draw K rectangles in N * M grid will be:
nCr(N-1, 2*k) * nCr(M-1, 2*k)
We can compute nCr using the Dynamic programming approach.




