Introduction:
We are given an integer ‘N’. We need to consider a N * N grid. We are currently at the top left corner of the grid. We need to find the number of ways by which we can reach the bottom right corner if we can make the right(i, j+1) or down(i+1, j) move. There is one condition that we cannot cross the diagonal while making any move.
Let us see a few examples:
Input 1: 3
Output 1: 2
Explanation 1:
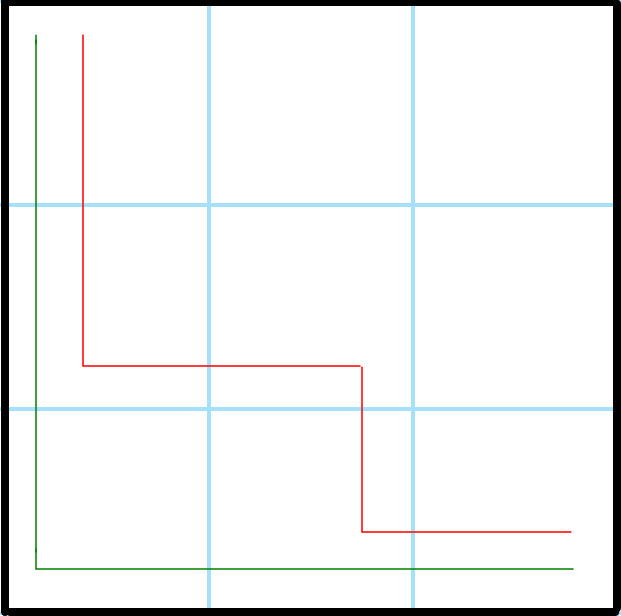
We can see the 2 paths in the red and green lines.
Input 2: 6
Output 2: 42
Input 3: 4
Output 3: 5
Also see, Euclid GCD Algorithm
Approach:
The number of downwards movements will always be greater than or equal to the rightward movements because we can not cross the main diagonal. It is a similar pattern to the Catalan’s number.
Based on the above observation we just need to find the Nth Catalan Number.
Also, let us find the answer for a few of the ‘N’ values.
N = 1 -> 1
N = 2 -> 1
N = 3 -> 2
N = 4 -> 5
N = 5 -> 14
N = 6 -> 42
Answer for N = (1 to 6) is following the Catalan Number Series
Nth Catalan Number (KN) = (2NCN ) / (N + 1), where 2NCN is a binomial coefficient.
Total number of ways = KN
Refer to the below implementation of the above approach to find the number of ways you can always stay either above or below the main diagonal
.
|
import java.util.*; class Main { static int binaryCoefficient(int n, int r) { int coeff = 1; int i; if (r > (n - r)) { // C(n, r) = C(n, n-r) r = (n - r); } for (i = 0; i < r; i++) { // [n * (n - 1) *---* (n - r + 1)] / [r * (r - 1) *----* 1] coeff *= (n - i); coeff /= (i + 1); } return coeff; } /* Function to calculate the total possible paths without crossing the diagonal */ static int totalWays(int n) { /* Update n to n - 1 as (N - 1) catalan number is the result */ n--; int fir, sec, res; // Stores 2nCn fir = binaryCoefficient(2 * n, n); // Stores Nth Catalan number sec = fir / (n + 1); // Stores the required answer res = sec; return res; } // Driver Code public static void main(String[] args) { int n = 5; /* Printing the total possible paths without crossing the diagonal */ System.out.print(totalWays(n)); } } |
Time Complexity: The time complexity for the above approach is O(N) (where ‘N’ is the input we are given for the matrix dimension) because we are only running an O(N) for loop for finding the Binomial Coefficient.
Space Complexity: The space complexity for the above approach is O(1) as we are using constant space for this solution