Introduction-
This blog will discuss the problem of finding an optimal sequence for AVL tree insertion. Before moving further, let’s see what an AVL Tree is.
“AVL trees, also known as self-balancing binary search trees, are a special type of binary search trees which adjust their height such that the difference of heights of left and right subtree of any node is either 0 or 1.”
Now, let’s understand the problem:
In this problem, we will be given an array of integers, and we have to find a sequence in which we should insert these integers into a binary search tree such that it will be an AVL tree without requiring any rotations to self-balance it.
Look at the following example for better understanding:
Suppose the following array of integers is given:
arr = {5, 4, 3, 2, 1}
Case 1: If we insert the integers in the given order, we will get the following binary search tree:
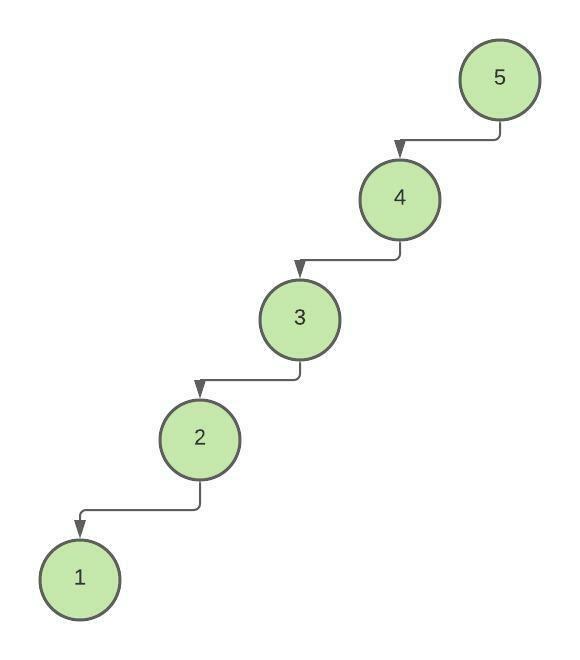
We can see that this binary search tree is not a balanced BST, so rotations are required to make it an AVL tree.
Case 2: If we insert the integers in the order {1, 2, 3, 4, 5}, we will get the following binary search tree:

We can see that this binary search tree is not a balanced BST, so rotations are required to make it an AVL tree.
Case 3: If we insert the integers in the order {3, 1, 4, 2, 5}, we will get the following binary search tree:

This is a balanced binary search tree, and no rotations are required to convert it into an AVL tree.
Hence, {3, 1, 4, 2, 5} can be the required optimal sequence for AVL tree insertion.
Now that we understand the problem let’s discuss the approach to solving it in the next section.
Solution Approach
This section will discuss the approach to find the optimal sequence for AVL tree insertion. To find the optimal sequence for AVL tree insertion, first create a balanced binary search tree (i.e., AVL tree) using the given integers. After creating the AVL tree from the given integers, find the level order traversal of the tree. If we insert the integers in that order, then the AVL tree will be created level by level. To construct an AVL tree using the given array of integers, we can sort the integers and use a recursive function in which we will find the middle element of the array and make it root and then call the function recursively to construct the left and right subtrees with the left and right half of the array integers respectively.




