Introduction
A Binary Search Tree (BST) is a tree in which the key of the nodes of the left sub-tree has a lower value than the key of its parent (root) node, and the key of the right sub-tree is greater than or equal to the key of its parent (root) node.
A binary Search Tree is a collection of nodes that are arranged in such a way that they retain BST properties.
This blog will discuss the problem of implementing Pair with a given sum in BST. We will discuss this article in detail.

Problem Statement
In this problem, we are given a sum and a BST as input, and we have to find the two node pair whose key value sum is equal to the given sum in Binary Search Tree (BST).
With some examples, let’s understand the problem pair with a given sum in Binary Search Tree ( BST).
Sample Examples
Example 1:
Input:
sum = 7
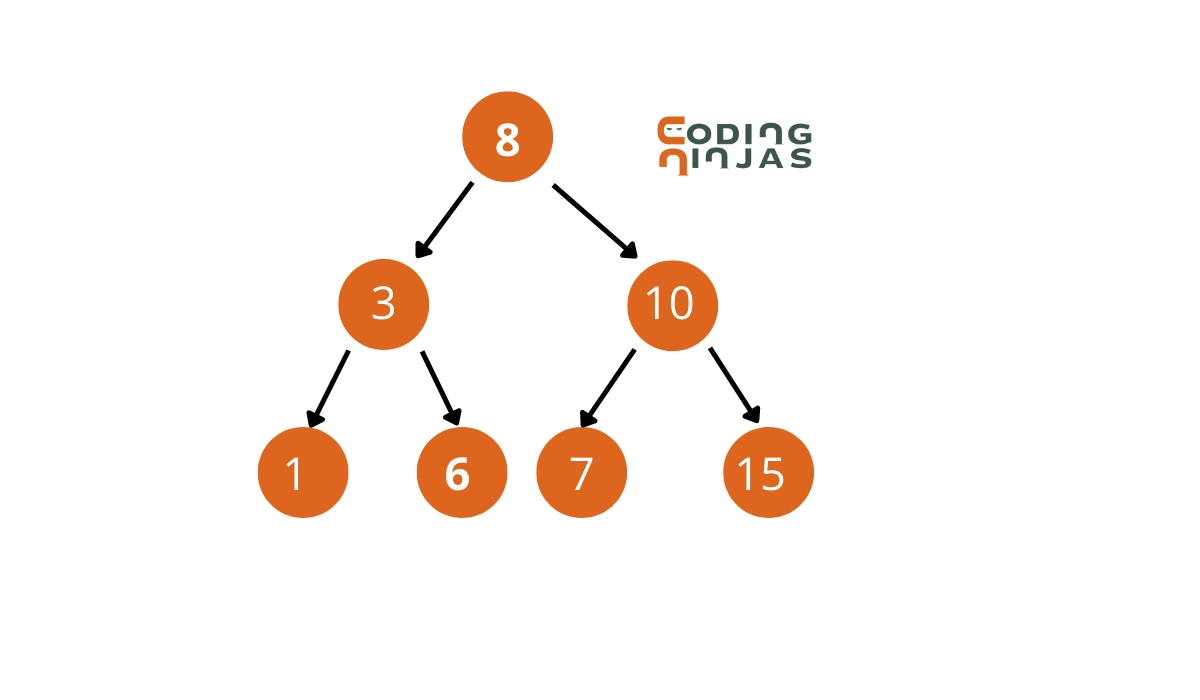
Output:
Pair with the given sum (1,6)
Explanation:
We will store the node of the tree in a set while traversing. If, for present node 1, there exists a node for which the sum of both nodes is equal to the target node, then we will return the pair.
Example 2:
Input:
sum = 13
Output:
Pair with the given sum (5,8)
Explanation:
We will store the node of the tree in a set while traversing. If for present node 5, there exists a node for which the sum of both nodes is equal to the target node, then we will return the pair.
Approach
We will discuss Hashing based approach. We traverse the binary search tree (BST) in order and insert the value of each node into a set. We will also look for any node with a difference between the given sum and the node's value in the set; if it is found, the Pair exists; otherwise, it does not. Let's see the algorithm for this approach.
Algorithm
✔️ Firstly, create a function to create a new BST node.
✔️ Create a Hash Set to insert the value of each node.
✔️ Now, we will check whether the node with a value equal to the difference between the sum and node value is present in the set or not.
✔️ If the node is found, then the Pair exists. Otherwise, it does not exist.
Implementation in Java
import java.util.*;
class test {
static class Node
{
int data;
Node left, right;
};
static Node New_Node(int data)
{
Node temp = new Node();
temp.data = data;
temp.left = null;
temp.right = null;
return temp;
}
static Node insert_node(Node root, int key) // function to insert node in BST
{
if (root == null)
{
return New_Node(key);
}
if (key < root.data)
{
root.left = insert_node(root.left, key);
}
else
{
root.right = insert_node(root.right, key);
}
return root;
}
static boolean findpair(Node root, int s,HashSet<Integer> set) // function to cjheck pair with given sum
{
if (root == null)
{
return false;
}
if (findpair(root.left, s, set))
{
return true;
}
if (set.contains(s - root.data))
{
System.out.println("Pair is found ("+ (s - root.data) + ", " + root.data + ")");
return true;
}
else
{
set.add(root.data);
}
return findpair(root.right, s, set);
}
static void findPairWithgivenSum(Node root, int s)
{
HashSet<Integer> set = new HashSet<Integer>();
if (!findpair(root, s, set))
{
System.out.print("Pairs do not exit"+ "\n");
}
}
public static void main(String[] args) // Driver class
{
Node root = null;
root = insert_node(root,8);
root = insert_node(root, 3);
root = insert_node(root, 10);
root = insert_node(root, 8);
root = insert_node(root, 1);
root = insert_node(root, 6);
root = insert_node(root, 7);
root = insert_node(root, 15);
int s = 7;
findPairWithgivenSum(root, s);
}
}
Output:
Pair is found (1, 6)Implementation in C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
Node* NewNode(int data)
{
Node* temp = (Node*)malloc(sizeof(Node));
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
Node* insert_node(Node* root, int key)
{
if (root == NULL)
{
return NewNode(key);
}
if (key < root->data)
{
root->left = insert_node(root->left, key);
}
else
{
root->right = insert_node(root->right, key);
}
return root;
}
bool findpair(Node* root, int s, unordered_set<int>& set)
{
if (root == NULL)
{
return false;
}
if (findpair(root->left, s, set))
{
return true;
}
if (set.find(s - root->data) != set.end())
{
cout << "Pair is found (" << s - root->data << ", " << root->data << ")" << endl;
return true;
}
else
{
set.insert(root->data);
}
return findpair(root->right, s, set);
}
void findPairWithGivenSum(Node* root, int s)
{
unordered_set<int> set;
if (!findpair(root, s, set))
{
cout << "Pairs do not exit" << endl;
}
}
// Driver code
int main()
{
Node* root = NULL;
root = insert_node(root,8);
root = insert_node(root, 3);
root = insert_node(root, 10);
root = insert_node(root, 8);
root = insert_node(root, 1);
root = insert_node(root, 6);
root = insert_node(root, 7);
root = insert_node(root, 15);
int s = 7;
findPairWithGivenSum(root, s);
return 0;
}
Output:
Pair is found (1, 6)
Time Complexity
The time complexity of the above approach for the problem of finding Pair with a given sum BST is O(n) as we have to traverse the tree nodes to check for the pairs whose sum is equal to the target sum.
Space Complexity
The space complexity of the above approach for the problem of finding Pair with a given sum BST is O(n) as we are using a set in this approach.




