Introduction
Deep neural networks may contain millions, even billions, of parameters or weights, making storage and computation significantly expensive and motivating a large body of work to reduce their complexity by using, e.g., sparsity inducing regularization. Parameter sharing and parameter tying is another well-known approach for controlling the complexity of Deep Neural Networks by forcing certain weights to share the same value. Specific forms of weight sharing are hard-wired to express certain invariances. One typical example is the shift-invariance of convolutional layers. However, other weights groups may be tied together during the learning process to reduce network complexity further.
Also Read, Resnet 50 Architecture, Difference between argument and parameter
Parameter Tying
Parameter tying is a regularization technique. We divide the parameters or weights of a machine learning model into groups by leveraging prior knowledge, and all parameters in each group are constrained to take the same value. In simple terms, we want to express that specific parameter should be close to each other.
Example
Two models perform the same classification task (with the same set of classes) but with different input data.
• Model A with parameters wt(A).
• Model B with parameters wt(B).
The two models hash the input to two different but related outputs.
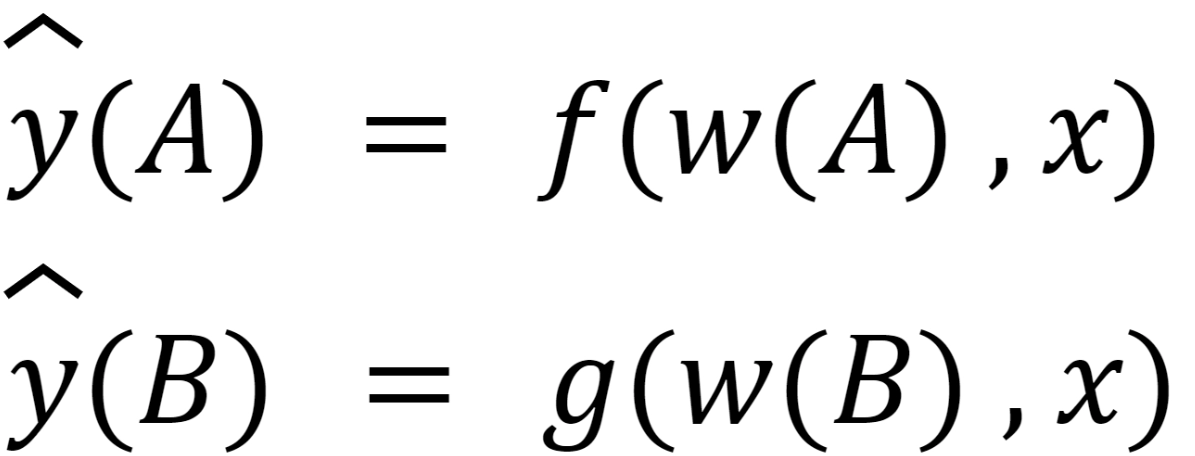
Some standard regularisers like l1 and l2 penalize model parameters for deviating from the fixed value of zero. One of the side effects of Lasso or group-Lasso regularization in learning a Deep Neural Networks is that there is a possibility that many of the parameters may become zero. Thus, reducing the amount of memory required to store the model and lowering the computational cost of applying it. A significant drawback of Lasso (or group-Lasso) regularization is that in the presence of groups of highly correlated features, it tends to select only one or an arbitrary convex combination of elements from each group. Moreover, the learning process of Lasso tends to be unstable because the subsets of parameters that end up selected may change dramatically with minor changes in the data or algorithmic procedure. In Deep Neural Networks, it is almost unavoidable to encounter correlated features due to the high dimensionality of the input to each layer and because neurons tend to adapt, producing strongly correlated features that we pass as an input to the subsequent layer.
To overcome the issues we face while using Lasso or group lasso is countered by a regularizer, the group version of the ordered weighted one norm, known as group-OWL (GrOWL). GrOWL supports sparsity and simultaneously learns which parameters should share a similar value. GrOWL has been effective in linear regression, identifying and coping with strongly correlated covariates. Unlike standard sparsity-inducing regularizers (e.g., Lasso), GrOWL eliminates unimportant neurons by setting all their weights to zero and explicitly identifies strongly correlated neurons by tying the corresponding weights to an expected value. This ability of GrOWL motivates the following two-stage procedure:
(i) use GrOWL regularization during training to simultaneously identify significant neurons and groups of parameters that should be tied together.
(ii) retrain the network, enforcing the structure unveiled in the previous phase, i.e., keeping only the significant neurons and implementing the learned tying structure.




