Table of contents

Problem Statement

Approach for Solution

Code

Dry-Run

Complexity

Frequently Asked Question

Key Takeaway

Last Updated: Mar 27, 2024

Path Requiring a Minimum Number of Jumps to Reach the End of the Array

Author Yogesh Kumar

Problem Statement

Here we have a problem statement, Paths requiring a minimum number of jumps to reach the end of the array.

Here we have the problem of finding all the possible paths, requiring minimum jumps to reach the end of the array. For better understanding, let’s discuss the problem with the help of an example.

Input Array: arr[]= { 3 , 3 , 0 , 2 , 1 , 0 }

Output : 0-> 3->5

Here above is the path we follow for 0-based indexing for the input array. The minimum value for the jump is 3, and there is only one path possible for the minimum jump to reach the end of the array.

Now understand it more descriptively:

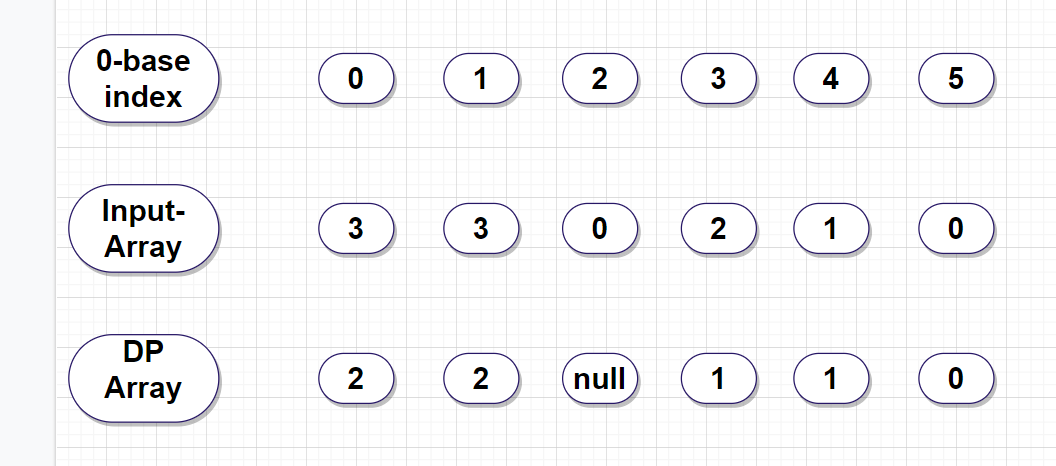
Here in the Input Array, we have given how to extend the index we may jump from the present index. I.e. for 0 indexes, we have a choice up to 0+3 =3 index value we go either 1, 2, or 3. In the similar way we have for the index 1, with value 1+3=4 index we either go to 2, 3 or 4, similar for the 2 indexes with 0 value we reside 2+0=2 index itself its a blockage, similar for 3 indexes with the value of jump 2, we go up to 3+2=5 index we have a choice for 4 or 5. For index value 4 with the value of jump 1, we have 4+1=5 index, similar to the last reaching index value 5 here we have 0 as always as we have reached the destination or end of the array.
Here in the Dp-Array, we are storing the minimum jumps we require to reach the destination of the array. That is the meaning of the Dp-Array, now. We go with the smaller problem to store the value, so we start filling the DP array in the backward direction.
For the storage in the backward direction, for index=5, as its last, we have itself at the last index, so in dp array which has information for minimum jumps to reach the destination index or end of array from their index, now for index=4, we have arr[4] =1, so we have max extent for the jump is 1, so in dp[4]=1.
Now for the index =3, we have arr[3]=2 we have extended up to 2 indexes, i.e. 4 or 5, if we have chosen 4 then we have to go 5 again, which require 2, as we choose 5 then it 1, so for that, we considered for the minimum part, so we choose 5 and dp[3]=1.
Now for the index =2, we have arr[2]=0, as we have an extent of jump value is 0, so we have a blockage, so dp[2]=null.
Now for the index=1, we have arr[1]=3, we have chosen for 2, 3 or 4 indexes as jump up to 3 indexes, so for we choose the minimum value plus additional itself own, now arr[2]=null, arr[3]=1 and arr[4]=1, as we have minimum 1 value we have a choice for both, we take any of the paths either by 3 or 4 value, so dp[1]=2.
Now for the index=0, we have the arr[0]=3 so we have 1, 2, or 3 choices, as seeing arr[1]=2, arr[2]=null, and arr[3]= 1, as seeing the value of all the three index value of array, we have a minimum at 3, i.e. 1 for reaching destination point with a minimum jump. So we choose the value 1, so dp[0]=2.

The above illustration shows the filling meaning for the Dp-Array, properly, if we iterate the same in the way, for minimum jump, we find that we have an answer column, with 0 -> 3 -> 5, we require a minimum 3 jumps to reach the end of the array.

Approach for Solution

Now let’s think about solving the problem in a better way; as we have to find the minimum jumps, path possible to reach the end of the array, we are getting the Dynamic Programming Approach for the minimal value of the jump to reach the end of the array.

Now understand the way of steps manner to solve the problem are as follow:-

Firstly we understand the meaning of the given input array, which shows the maximum number of jumps or steps we take forward from that element at every index.
Then it just became the problem of finding the minimum number of jumps to reach the end of the array, i.e. Jump Game II but here, we have to also trace the path for that finding.
For that, we declare a dp array for finding the minimum number of jumps to reach the destination of the array at every index; how many jumps are required? We have to calculate it. This can be done by the concept of dynamic programming for solving the small problem first. For the bigger problem, we have started filling the DP-array from the backward direction, which implementation is explained above in the Explanation of the problem statement.
Now, after creating the Dp- Array, we have the process of reverse engineering sort of thing, as we fill Dp- Array in backward then start traversing the Dp-Array in forwarding direction.
To do reverse engineering, we are required to store some Information, to aim our answer to print the possible path for minimum jump, so we declare another class for which it has the information of index we are working, allowed_jump at particular index from the input array, minimum_jum_calculated for each index in Dp-Array to reach the end of the array and path_calculated_soFar for the possible pathfinding for the minimum jump.
In this way, we followed the steps and did our task.

Code

import java.util.ArrayDeque;
import java.util.Arrays;

public class path_possible {
  // Creating a Information class for storing
  //index, allowed_jump, minimum_jump_calculated and path_calculated_soFar
  public static class Information{
      int index;
      int allowed_jump;
      int minimum_jump_calculate;
      String path_calculated_soFar;
      Information(int index,int allowed_jump,int minimum_jump_calculate,String path_calculated_soFar){
          this.index=index;
          this.allowed_jump=allowed_jump;
          this.minimum_jump_calculate=minimum_jump_calculate;
          this.path_calculated_soFar=path_calculated_soFar;
      }
  }
  public static void PathPossible(int [] arr){
      // We are creating Integer array as we can compare with the null value
      Integer [] dp=new Integer[arr.length];
      // At last point we are not going , as we move we get out of index range so minimum jump is 0
      dp[arr.length-1]=0;
      // Solving the problem for in the direction of smaller problem
      for(int i= arr.length-2;i>=0;i--){
          int extent_of_jump=arr[i];
          int min=Integer.MAX_VALUE;
          // Filling the dp array for the minimum number of possible jumps possible at
          // particular index.
          for(int j=1;j<=extent_of_jump&&i+j< arr.length;j++){
              if(dp[i+j]!=null && dp[i+j]<min){
                  min=dp[i+j];
              }
          }
          // Check for if all the path for jump is block for that index then we do nothing with min value
          if(min!=Integer.MAX_VALUE){
              dp[i]=min+1;
          }
      }
      // Creating a Array Deque , and storing the information
      // index, allowed_jump, minimum_jump_calculated and path_calculated_soFar
      //By creating another class information.
      ArrayDeque<Information> dequeue=new ArrayDeque<>();
      dequeue.add(new Information(0,arr[0],dp[0],0+""));
      while (dequeue.size()>0){
          Information info=dequeue.removeFirst();
          if(info.minimum_jump_calculate==0){
              System.out.println(info.path_calculated_soFar);
          }
          for(int j=1;j<=info.allowed_jump && info.index+j< arr.length;j++){
              int curr_index= info.index+j;
              // we checking for the if we allowed to move and we also have the option for checking is it
              // suitable move with minimum jump.
              if(dp[curr_index]!=null && dp[curr_index]==info.minimum_jump_calculate-1){
                  // If it's a suitable move for the answer then we add the path index for the number.
                  dequeue.add(new Information(curr_index,arr[curr_index],
                          dp[curr_index],info.path_calculated_soFar+"->"+curr_index));
              }
          }
      }
  }
  public static void main(String[] args){
      // Creating 0-based indexing array
      int [] arr={3,3,0,2,1,0};
      // Calling a PathPossible which prints out the possible path for minimum jump.
      PathPossible(arr);
  }
}

You can also try this code with Online Java Compiler

Run Code

Dry-Run

Now understand the run-way of code using the example given below:-

Input Array : { 3 , 3 , 0 , 2 , 1 , 0 }

We have given an input array that shows the maximum step from the next index in the forward direction.

Let’sLet’s get with the implementation part:-

Firstly we have created a dynamic Array for the minimum number of jumps to reach the destination or end of the array and store the value in it explained the filling of the Dp-Array is already shown.
Now we are creating an Information class that has index storage, allowed_jump, minimum_jump_calculated, and path_calculated_soFar.
Now, after that, we have to track the path for the target of the question.
For reverse engineering, firstly, we create a deque with the Information class data. Then, we push the 0 index allowed_jump, 0 indexes minimum_jump_calculated, and empty string.
Then through the while loop, we run a loop by picking the first element, checking the possible chance for the allowed, and choosing the minimum one.
This step continues and ends when we find the minimum jump calculated value as 0, we print the path_calculated_soFar.

Now go with example dry-run:-

For the first time, we have an element in the queue in order of index, allowed_jump, minimum_jump_calculated and path_calculated_soFar.

0-3-2 (0)

(Now we have 3 max jumps allowed with two paths 1 and 3 and 2 is blocked)

3-2-1 (0->3)

(Now we have moved to index three as, with two paths via 1 or 3, 3 has minimum jumps for reach end so we choose 3 with our answer, and allowed_jump is 2).

5-0-0(0->3->5)

(Now we reach the last endpoint as info.minimum_jump_calaculate==0)

Now we print our answer and are done with our task.

Complexity

Time Complexity for the problem is O(N^2). As we are working on the Input Array, Dp-Array, we are creating a Dynamic Array Deque and performing the task for finding the path_calculated_soFar; for that, we are doing quadratic times operation.

Now For the Space Complexity, we have O(N) one for the extra Dp-Array, as we have Dynamic Deque, which also requires N size memory so that our Space Complexity is O(N).

Frequently Asked Question

1). What are Time Complexity and Space Complexity?

Ans: Time Complexity is O(N^2), and Space Complexity is O(N).

2). What is Dynamic Programming?

Ans: Mathematical and Computer-optimized method to solve the program.

3). What is ArrayDeque in Java?

Ans: ArrayDeque is a class in java that provides the Dynamic Array that can be used as a Deque.

Key Takeaway

In this problem, we solve the question using the concept of Dynamic Programming in which we use the idea of ArrayDeque, which provides the Dynamic Array that can be used as a Deque. In this problem, we print the best minimal path required to start running from the start of the array to the end, with a minimum jump, with a trace path also printed for it.

Live masterclass

Switch from service to product-based MAANG companies

by Pranav Malik, SDE3 @ Oracle, Ex- Microsoft

17 Oct, 2024

01:30 PM

46+ registered

Predictive Analytics: Forecast ticket sales for an event like Coldplay

by Megna Roy, Data Analyst @ Amazon

15 Oct, 2024

01:30 PM

197+ registered

Switch from service to product-based MAANG companies

by Pranav Malik, SDE3 @ Oracle, Ex- Microsoft

17 Oct, 2024

01:30 PM

46+ registered

Predictive Analytics: Forecast ticket sales for an event like Coldplay

by Megna Roy, Data Analyst @ Amazon

15 Oct, 2024

01:30 PM

197+ registered

View more events