Introduction
The one thing we all see all around us is data, data surrounds us, and sometimes understanding data is crucial. There are many ways to represent the data. We can represent the data in text or virtual representation. So, where is the need for a graph?
Graphs are the textual representation of data with significantly less space required and can represent small data efficiently so that everyone can understand it.
The graph contains vertices as the nodes, and edges are the lines connecting different vertices representing the data. The graph also has different types to represent data: planar and non-planar graphs.
We will learn more about planar and non-planar graphs while moving further with the blog, so let's move on with our topic without wasting any time.
Planar Graph
It is the type of graph that can be drawn in a plane with no edge overlap or cross each other.
Example:
Here we will discuss the example of a planar graph with four vertices.
And can also connect like this:
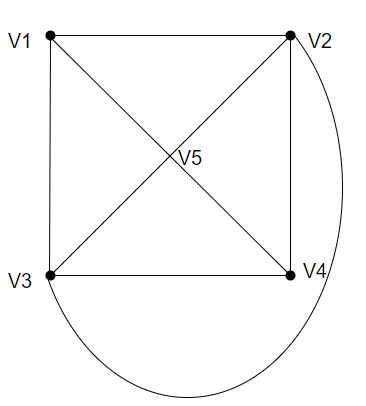
Here first, we connected internally then externally.
Regions of a Graph
To understand the region in a graph, assume a graph G = (V, E) where V is the number of vertices and E is the number of edges present in the graph. A region is defined as the area of the plane in the graph which is enclosed or surrounded by edges and can not be subdivided further.
A planar graph divides the graph into one or more regions, one of which is an infinite region. Finite and infinite areas are explained below:
Finite Region
If the area of the region in the graph or any plane is finite, then it is known as finite region.
The planar graph can have more than one finite region.
Infinite Region
If the area of the region in the graph or any plane is infinite, then it is known as infinite region. The planar graph has only one infinite region.
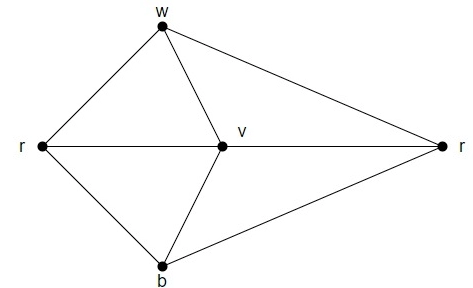
Example
Consider the graph given below. Find the name and number of finite and infinite regions.
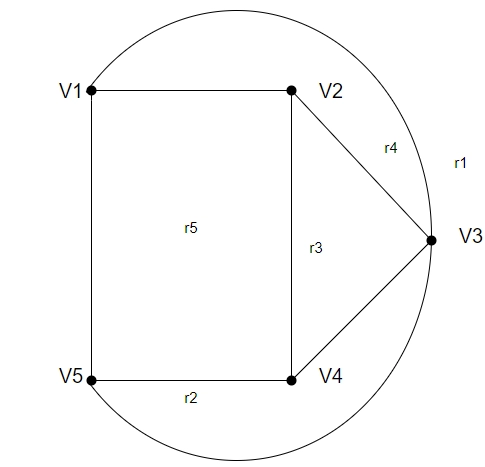
Solution:
There are five regions present in the above graph r1, r2, r3, r4, r5.
Among the above five regions, r2, r3, r4, r5 are the finite region.
Whereas r1 is the infinite region.
Properties of Planar Graphs
There are some properties of a planar graph. We will list all of them below:
-
If a connected planar graph G has r regions and e edges, then r ≤
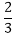 e.
e.
- If a connected planar graph G has v vertices, r regions, and e edges, then v-e+r=2.
- If a connected planar graph G has v vertices and e edges, then 3v-e>=6.
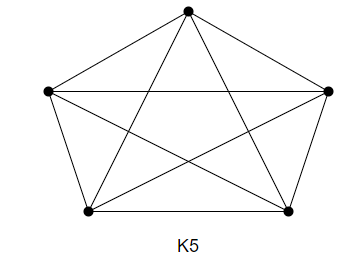
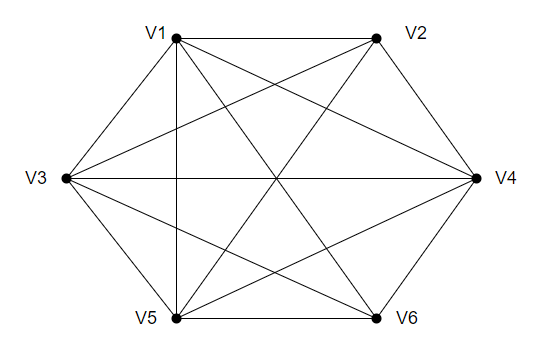
- A complete graph Kn is said to be planar if and only if n<5.
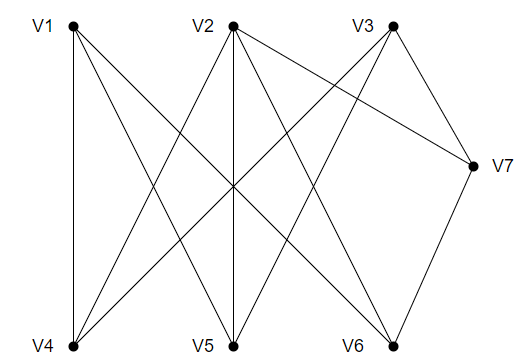
- A complete bipartite graph Kmn is said to be planar if and only if n>3 or m<3.
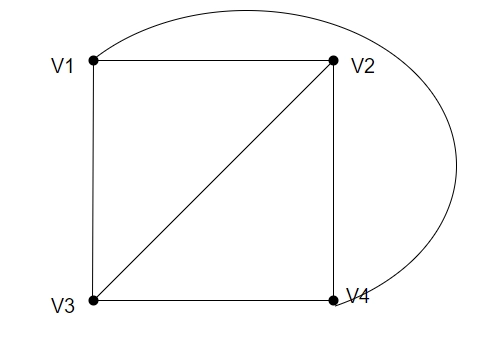
Example
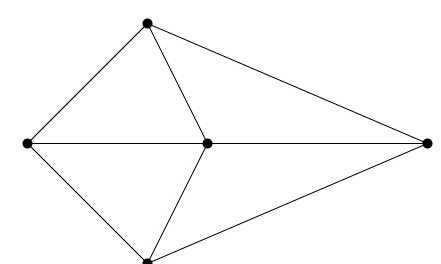
Consider the graph given below and prove that it is planar.

In the above graph, there are four vertices and six edges. So 3v-e = 3*4-6=6, which holds the property three hence it is a planar graph.