Plates Between Candles - Naukri Code 360

Question

There is a long table with plates and candles placed in a line on the top of it. You're given a 0-indexed string s that only contains the letters'*' and '|,' with a '*' representing a plate and a '|' representing a candle.

In addition, you are given a 0-indexed 2D integer array queries, where queries[i] = [lefti, righti] signifies the substring s[lefti...righti] (inclusive).

You have to count the number of plates between candles in each substring for each query. If the given substring contains at least one candle to its left and one to its right, the plate is considered between candles.

Alert Ninjas: Don’t stop now! Enroll in the Competitive Programming course today and start coding. Learn the art of writing time and space-efficient code and compete in code competitions worldwide.

Input: A string s, a vector of strings of queries.

Output: Return an answer array where answer[i] is the answer to the ith query.

Example 1

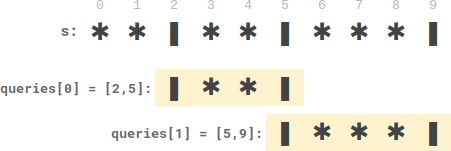
Input: s = "**|**|***|", queries = [[2,5],[5,9]]

Output: [2,3]

Explanation:

-There are two plates between candles in queries[0].

-There are three plates between candles in queries[1].

Example 2

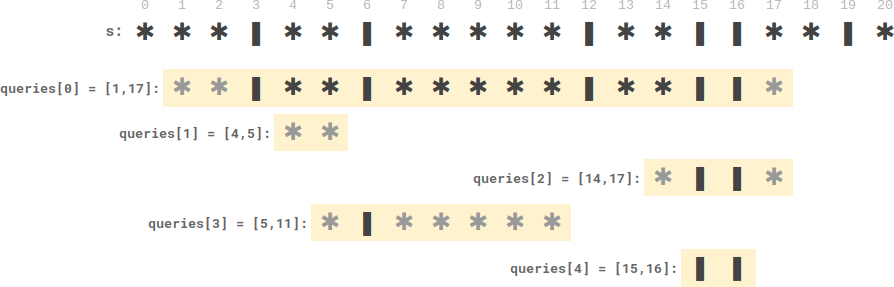
Input: s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11]]

Output: [9,0,0,0]

Explanation:

- There are nine plates between candles in queries[0].

- There are no plates between candles in the remaining queries.

Solution

Observation:

This problem requires us to find a sum between a range that should immediately hint prefix sum. This will result in the constant time calculation of a query.

Idea:

The idea is to find the closest candles at the boundary that get us in the range for each query. This means we need to find the nearest left candle of the leftmost index and the nearest right candle of the rightmost index. And return the number of plates between these leftmost and rightmost candles.

We maintained three arrays prev, next, and preSum:

prev[i] will store the nearest left candle.
next[i] will store the nearest right candle.
preSum[i] will store the number of plates up to index i.

C++

vector<int> platesBetweenCandles(string s, vector<vector<int>>& queries) {

  int q = queries.size();
  int l = s.length();

vector<int> ans;
vector<int> prev(l);
vector<int> next(l);
vector<int> preSum(l);

  int p=-1, nxt = -1;

  // calculating prev candle up to this index.
  for(int i = 0; i < l ; i++){

  if(s[i] == '|'){
p = i;
}
prev[i] = p;
}
  //Calculating next candle from this index.

  for(int i = l-1 ;i >= 0 ; i--){

  if(s[i] == '|'){
nxt = i;
}
next[i] = nxt;
}

  int c=0;

  // calculating the number of stars between these indices.
  for(int i = 0; i < l ; i++){

  if(s[i] == '*'){
c++;
}
preSum[i] = c;
}

  // calculating ans.
  for(int k = 0 ; k < q ; k++){

  int i = queries[k][0];
  int j = queries[k][1];

  int right = prev[j];// position of left candle.
  int left = next[i];// position of right candle.
  //cout<<right<<left;

  if(left == -1 || right == -1 || left > right){
ans.push_back(0);
}
  else{
ans.push_back(preSum[right] - preSum[left]);
}
}
  return ans;
}

Time Complexity: O(N+Q)

Space Complexity: O(N)

Also check out - Substr C++ and Rabin Karp Algorithm

Key takeaways

Here we solved a medium leveled programming question using Dynamic Programming. Join this Master Class on DP by Coding Ninjas and become a Ninja coder.

We solved it in O(N) space complexity. Can you further reduce the space complexity?

Start coding today, practice more Data Structures and Algorithms problems.

Recommended Readings:

Happy Coding!