What is the alternative algorithm of the Knuth-Morris-Pratt algorithm?

Robin-Karp algorithm is an alternative to the KMP algorithm.

What is the proper prefix of a string?

The proper prefix of a string is a substring that is not equal to the length of the string itself.

Table of contents

Introduction

Algorithm

Brute force approach

Optimized approach:

Code

Complexity analysis

Application

Code

FAQs

10.

Key Takeaways

Last Updated: Mar 27, 2024

Prefix function - Knuth-Morris-Pratt Algorithm

Q: What is the application of the KMP algorithm?

KMP algorithm is used for searching a substring in a string, the number of unique substrings in a string, pattern matching problem.

Author Malay Gain

Introduction

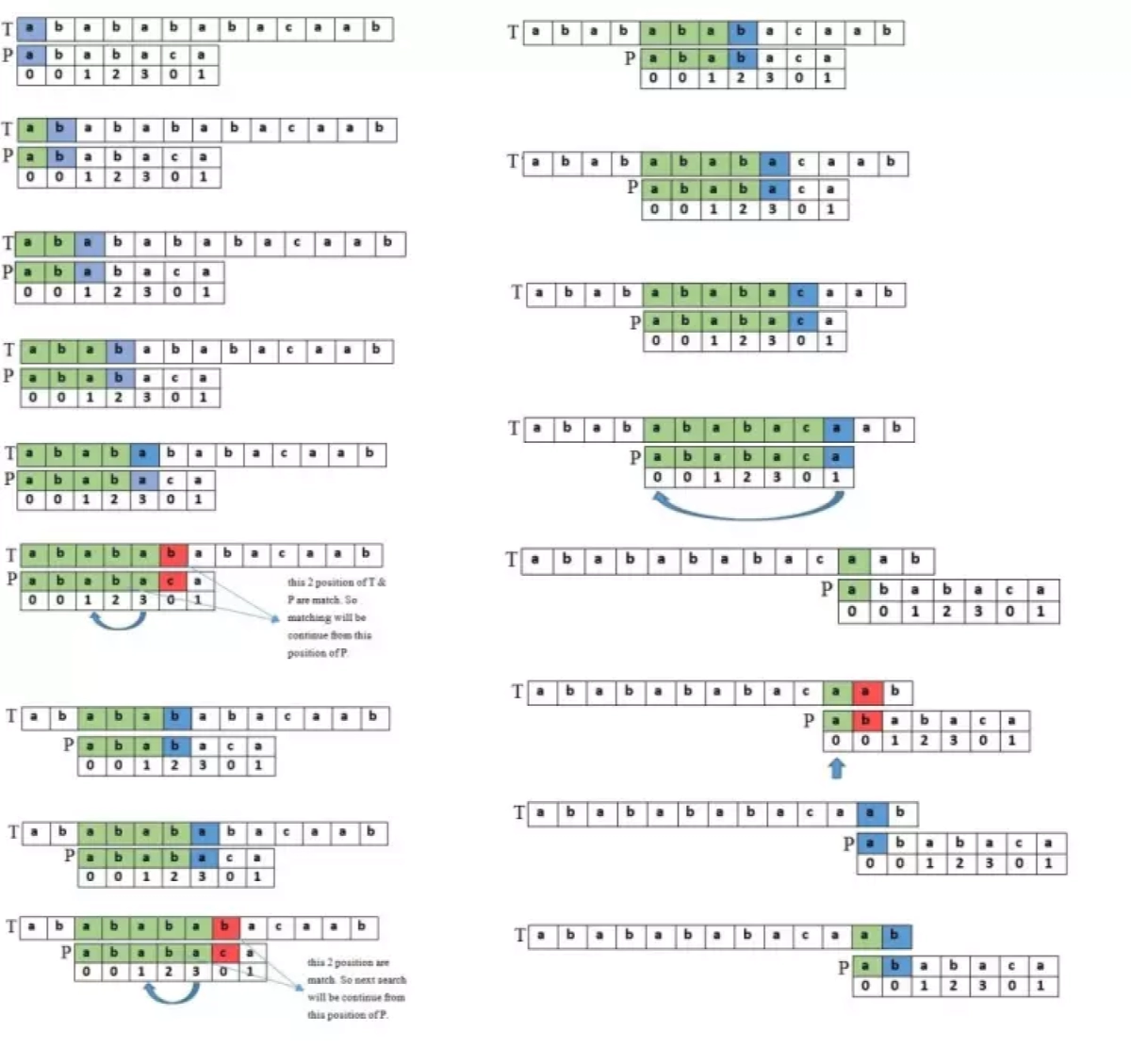
KMP is the most popular substring search algorithm in linear time. This algorithm is used for finding linear time solutions of various string-related problems such as searching substring in a string, the number of unique substrings in a string, pattern matching problem, etc.

Algorithm

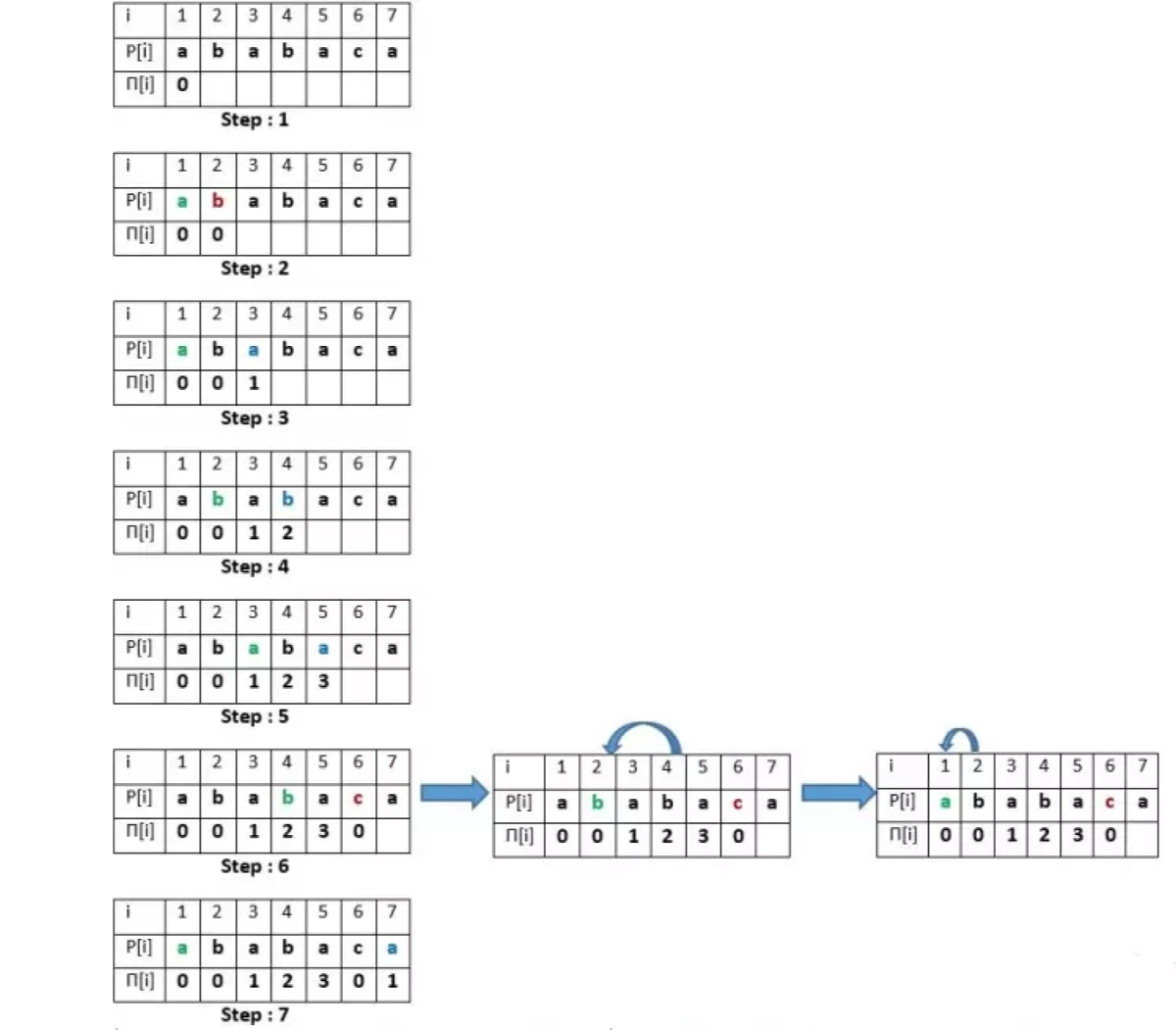
The main component of the KMP algorithm is the prefix function. It is defined as for a string s of length n, π[i] is the length of the longest proper prefix of the substring s[0…i], which is also a suffix of this substring where the proper prefix of a string is a prefix that is not equal to the string itself. π[i] is the ith element of an n-length array π. By definition, π[0]=0.

π[i]= max

k=0...i

k : s[0…k−1]=s[i−(k−1)…i],

where s[0…k−1] is the proper prefix and s[i−(k−1)…i] is the suffix of length k of the string s.

e.g for string "ababaca", prefix function array π is [0,0,1,2,3,0,1]

source

Brute force approach

vector<int> prefix_function(string s)
{
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 0; i < n; i++)
  for (int k = 0; k <= i; k++)
{
if (s.substr(0, k) == s.substr(i-k+1, k))
{
pi[i] = k;
}
}


  return pi;
}

It takes O(n3) in the worst case.

Optimized approach:

At first, compute the prefix values π[i] in a loop by iterating from i=1 to i=n−1 (π[0] is assigned with 0).
To calculate the current value π[i], set the variable j denoting the length of the best suffix for i−1. Initially, j=π[i−1].
Test if the suffix of substring s[0....i] of length j+1 is also a prefix of the substring s[0....i] by comparing s[j] and s[i]. If they are equal, we assign π[i]=j+1 (the values of the prefix function can only increase by at most one); otherwise, reduce j to π[j−1] ( greatest k<j, for which the prefix property holds is π[j−1]) and repeat this step.
If length j=0 is reached and still don't have a match, then assign π[i]=0 and go to the next index i+1

Code

vector<int> prefix_function(string s)
{
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++)
{
  int j = pi[i-1];
  while (j > 0 && s[i] != s[j])
j = pi[j-1];
  if (s[i] == s[j])
j++;
pi[i] = j;
}
  return pi;
}

Complexity analysis

The KMP algorithm takes O(n) time in the worst case and space complexity is also O(n) for using an extra array of length n.

Also check out - Substr C++, and Euclid GCD Algorithm

Application

Searching a substring in a string

Searching a pattern P in string S using the ∏ function is just like making the ∏ function. If we get any difference in S and P, we can jump on a character in S with the help of ∏ function because we already equaled the suffix and prefix. Go through the below example for understanding how prefix function is used for pattern matching.

source

Code

#include<iostream>
using namespace std;

void findPrefix(string P, int m, int prefArray[]) {
int length = 0;
prefArray[0] = 0;   //first place is always 0 as no prefix

for(int i = 1; i<m; i++) {
  if(P[i] == P[length]) {
length++;
prefArray[i] = length;
}else {
  if(length != 0) {
length = prefArray[length - 1];
i--;   //decrease i to avoid effect of increasing after iteration
}else
prefArray[i] = 0;
}
}
}

void KMPSearch(string S, string P, int *locArray, int &loc) {
int n, m, i = 0, j = 0;
n = S.size();
m = P.size();
int prefixArray[m];   //prefix(?) array as same size of P
findPrefix(P, m, prefixArray);
loc = 0;

while(i < n) {
  if(S[i] == P[j]) {
i++;
j++;
}

  if(j == m) {
locArray[loc] = i-j;   //item found at i-j position.
loc++;
j = prefixArray[j-1];   //get the prefix length from array
}else if(i < n && P[j] != S[i]) {
  if(j != 0)
j = prefixArray[j-1];
  else
i++;
}
}
}

int main() {
string str = "aaaabaaaaabbbaaaab";
string patt = "aaab";
int locationArray[str.size()]; // array to store the start locations from where the pattern matched
int index;
KMPSearch(str, patt, locationArray, index);

for(int i = 0; i<index; i++) {
  cout << "Pattern found at location: " <<locationArray[i] << endl;
}
}

Output

Pattern found at location: 1
Pattern found at location: 7
Pattern found at location: 14

Prims and Kruskal Algorithm

FAQs

What is the application of the KMP algorithm?
KMP algorithm is used for searching a substring in a string, the number of unique substrings in a string, pattern matching problem.
What is the alternative algorithm of the Knuth-Morris-Pratt algorithm?
Robin-Karp algorithm is an alternative to the KMP algorithm.
What is the proper prefix of a string?
The proper prefix of a string is a substring that is not equal to the length of the string itself.

Key Takeaways

This article covered the KMP algorithm. We have learned about the algorithm to apply it for solving various string-related problems.

Check out this problem - Longest Common Prefix

Now, you can practice and solve a wide range of string-related coding questions commonly asked in interviews in Coding Ninjas Studio. Along with coding questions, we can also find the interview experience of scholars working in renowned product-based companies here.

Happy learning!

Live masterclass

Switch from non tech to high paying data analytics profile

by Alka Pandey, Data Scientist @ Hindustan Unilever

09 Oct, 2024

01:30 PM

117+ registered

Master PowerBI using Netflix Data

by Ashwin Goyal, Product @ HRS Group, Ex - Udaan, OYO

08 Oct, 2024

01:30 PM

586+ registered

Switch from non tech to high paying data analytics profile

by Alka Pandey, Data Scientist @ Hindustan Unilever

09 Oct, 2024

01:30 PM

117+ registered

Master PowerBI using Netflix Data

by Ashwin Goyal, Product @ HRS Group, Ex - Udaan, OYO

08 Oct, 2024

01:30 PM

586+ registered

View more events