Table of contents

Introduction:

Naive Primality Test

2.1.

Program

2.2.

Input:

2.3.

Output:

2.4.

Time Complexity

2.5.

Space Complexity:

Optimized Approach

3.1.

Program

3.2.

Input:

3.3.

Output:

3.4.

Time Complexity

3.5.

Space Complexity:

Fermat’s Little Theorem:

4.1.

Program

4.2.

Input:

4.3.

Output:

4.4.

Time Complexity:

4.5.

Space Complexity:

Practice Problems:

Key Takeaways:

Last Updated: Mar 27, 2024

Primality Tests

Author Husen Kagdi

Introduction:

Mohammed and Ali were two friends who lived in Nazak. Recently they have learned the difference between prime numbers and composite numbers in their school. They have taught how to check if a number is prime or not in a naive way. The method says we must iterate through 2 to N/2 and check whether ‘N’ is divisible by at least one of these numbers. If yes, then it is a composite number. Else, if it is divisible by none of them, then it is a prime number.

Here ‘N’ is the given number upon which the primality test needs to be conducted. Given a large number, this would consume a lot of time. They wondered whether there exists a better way to do the primality test. After a lot of research, they found out that Fermat’s Primality Test can help them in the task.

In this blog, we will discuss the idea behind Fermat’s primality test as well as its implementation in C++. But before that, let us first see the naive approach of the primality test.

Naive Primality Test

Given a number of ‘N’, we need to check if it is a prime or not. To solve this problem, one can think of a naive method of iterating through 2 to N/2 and check if any of them divides ‘N’. If yes, it is not prime. Else it is a prime number.

The C++ implementation of the above idea is provided below:

Program

#include <bits/stdc++.h>
using namespace std;

bool isPrime(int N)
{
if (N == 1)
{
return false;
}

  for (int i = 2; i <= N / 2; i++)
{
  if (N % i == 0)
{
  return false;
}
}
  return true;
}

int main()
{
  cout << "Enter the number to check its primality: ";

  int N;
  cin >> N;

  if (isPrime(N))
{
  cout << "Yes, " << N << " is a prime number." << endl;
}

  else
{
  cout << "No, " << N << " is not a prime number." << endl;
}
  cout << endl;
  return 0;
}

Input:

Enter the number to check its primality: 83

Output:

No, 83 is not a prime number.

Time Complexity

O(N), where ‘N’ is the given number.

It is because we are looping from 2 to N/2.

Space Complexity:

O(1).

As we are not using any extra space.

Also see, Euclid GCD Algorithm

Optimized Approach

Now let us discuss a better approach. It is not required to iterate to N/2. We can just iterate from two till SquareRoot(N). It is because the factor of a number occurs in pairs. So, if X is a factor of N, then N / X is also a factor of N. Therefore if we iterate from 2 till SquareRoot(N), all the factors will be covered.

Program

#include <bits/stdc++.h>
using namespace std;

bool isPrime(int N)
{
if (N == 1)
{
return false;
}

  for (int i = 2; i * i <= N; i++)
{
  if (N % i == 0)
{
  return false;
}
}
  return true;
}

int main()
{
  cout << "Enter the number to check its primality: ";

  int N;
  cin >> N;

  if (isPrime(N))
{
  cout << "Yes, " << N << " is a prime number" << endl;
}

  else
{
  cout << "No, " << N << " is not a prime number" << endl;
}
  cout << endl;
  return 0;
}

Input:

Enter the number to check its primality: 101

Output:

Yes, 101 is a prime number.

Time Complexity

O(sqrt(N)), where ‘N’ is the given number.

It is because we are looping from 2 to square root(N).

Space Complexity:

O(1).

As we are not using any extra space.

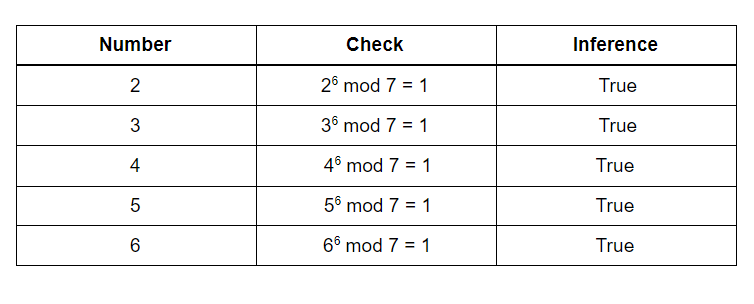
Now let us discuss Fermat’s primality test. This method is probabilistic and is based on Fermat’s Little Theorem.

Fermat’s Little Theorem:

Fermat's Little Theorem states that If ‘N’ is a prime number, then for every ‘X’ coprime with ‘N’ and 1 < X < N - 1.

X^{N - 1} mod N = 1

We can use this result to deduce whether a number is prime or not.

For example:

Let us consider the number 7. Then, numbers in the range (1, 6) coprime with 7 are 2, 3, 4, and 5.

Since for every coprime X > 1 and X < 7, X⁶ mod 7 == 1. Therefore, 7 is a prime number, which is true.

If the remainder is always 1, then there are high chances that it is a prime. However, it satisfies some composite numbers also. Since it is a probabilistic model, there are some inaccuracies. Hence, we make several iterations to determine the validity of our result.

Given below is an implementation of Fermat’s primality test.

Program

#include <bits/stdc++.h>
using namespace std;

int power(int x, int m, int n)
{
  int ans = 1;
x = x % n;

  if (x == 0) {
  return 0;
}

  while (m > 0)
{
  if (m & 1) {
ans = (ans * x) % n;
}

m = m >> 1;
x = (x * x) % n;
}
  return ans;
}

int gcd(int x, int y)
{
  if (y == 0)
{
  return x;
}
  return gcd(y, x % y);
}

bool isPrime(int n, int iterations = 5)
{
  if (n <= 1 || n == 4) {
  return false;
}

if (n <= 3) {
return true;
}

  while (iterations)
{
  int x = 2 + rand() % (n - 3);

  if (gcd(n, x) != 1) {
  continue;
}

  if (power(x, n - 1, n) != 1) {
  return false;
}

iterations--;
}

  return true;
}

int main()
{
  cout << "Enter the number to check its primality: ";

  int N;
  cin >> N;

  if (isPrime(N))
{
  cout << "Yes, " << N << " is a prime number" << endl;
}
  else
{
  cout << "No, " << N << " is not a prime number" << endl;
}
  cout << endl;
  return 0;
}

Input:

Enter the number to check its primality: 1013

Output:

Yes, 1013 is a prime number.

Time Complexity:

O(K * log(N)), where ‘K’ is the number of iterations and ‘N’ is the given number.

It is because we are making ‘K’ iterations and within an iteration, O(log(N)) time is consumed due to gcd() and power() functions.

This is a probabilistic method so that it might give wrong results for some test cases. Suppose we increase the value of K, accuracy increases. But the time taken also increases.

Space Complexity:

O(1).

As no auxiliary space has been used.

Practice Problems:

Would you mind navigating to our coding platform Coding Ninjas Studio and practice some problems to gain expertise in number theory concepts.

Key Takeaways:

In this blog, we learned how to check whether a given number is prime or not using three different methods. We also learned how to implement them in C++. After solving the practice problems, your knowledge in Number Systems will be enhanced. Thus a new feather to your cap of expertise will be added.

Thank You and Happy Coding!

By: Husen Kagdi