Introduction
Data structure and algorithms are one of the most important topics to understand if you want to work for a top product-based company. To have a complete understanding of DSA, you must solve a variety of code challenges. In this blog, we'll look at a coding problem in which we need to print the nodes that are exactly K distance away from the leaf node in our binary tree.
Problem Statement
Ninja has given you an integer K and a binary tree. Your task is to print all the nodes present in the binary tree that are exactly K distance away from a leaf node. In this case, k distance away from a leaf denotes k levels higher than a leaf node.
Sample Examples
Input
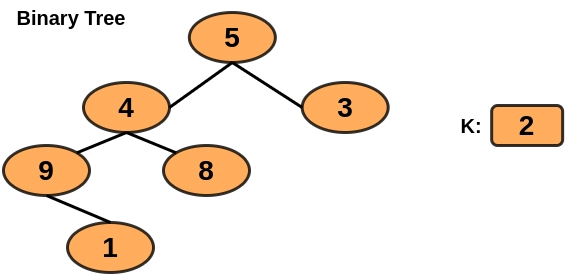
Output

Explanation
Node 4 and node 5 are exactly 2 distances away from leaf nodes 1, 8 and 3.
Example 2
Input
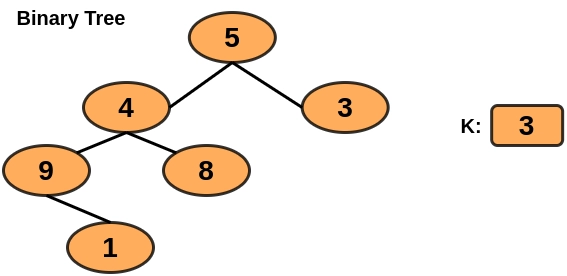
Output

Explanation
Only node 5 is 3 distance away from the leaf node.
Approach
Create two arrays one will store the path to the node and the other one will be used to keep track of the visited nodes. If the current node is null then get the node at distance K from the current node using the path array and print it on the screen otherwise call the function recursively with child nodes.
Algorithm
ALGORITHM(node, path[], visited[], len, k)
if node is null:
return;
path[len] <- node->data
visited[len] <- false
len <- len + 1
if node->left is NULL and node->right is NULL and len - k - 1 >= 0 and visited[len - k - 1] is false:
print (path[len - k - 1])
visited[len - k - 1] <- true
returnImplementation in C++
#include <bits/stdc++.h>
using namespace std;
// our node
class Node
{
public:
int data;
Node *left;
Node *right;
Node(int data)
{
this->data = data;
left = nullptr;
right = nullptr;
}
};
/*
function to print all nodes that are exactly K distance away from leaf node.
here variable Path is used to store the ancestors of a node and
the visited array keeps track of visited nodes.
len is used to keep track of distance from a node
*/
void k_distance_from_leaf(Node *node, vector<int> &path, vector<bool> &visited,
int len, int k)
{
// return null if root node is null
if (node == nullptr)
return;
/* appending current Node to the path */
path[len] = node->data;
visited[len] = false;
len++;
// if current node is leaf node then print its ancestors that are K distance away
if (node->left == nullptr && node->right == nullptr && len - k - 1 >= 0 && visited[len - k - 1] == false)
{
cout << path[len - k - 1] << " ";
visited[len - k - 1] = true;
return;
}
// if current node is not a leaf node then
// call the function with its child nodes
k_distance_from_leaf(node->left, path, visited, len, k);
k_distance_from_leaf(node->right, path, visited, len, k);
}
// main function
int main()
{
int k = 2;
Node *root = new Node(5);
root->left = new Node(4);
root->right = new Node(3);
root->left->left = new Node(9);
root->left->right = new Node(8);
root->left->left->right = new Node(1);
cout << "Nodes at distance " << k << " from leaf node: ";
// maximum height of tree
int max_height = 10000;
vector<int> path(max_height);
vector<bool> visited(max_height, false);
k_distance_from_leaf(root, path, visited, 0, k);
cout << endl;
return 0;
}
Output
Nodes at distance 2 from leaf node: 4 5 Time Complexity
The time complexity of the above program is O(n) as we are only doing a simple tree traversal.
Space Complexity
We are using visited and path arrays to store the details. So, the space complexity of the above program is O(max_height), where max_height is the maximum height of the tree defined in the program.




