Introduction 🤓
The problem to print BST keys in the given valid range is a very basic BST problem. When you start BST, you usually come across this.

This article will discuss how to print BST keys in the given valid range. We will use two approaches to find a solution to this problem. The interesting part is both of the approaches will have the same time complexity but different space complexities. This is the reason it is usually asked in interviews. So without any further ado. Let’s get started!

Problem Statement 🤔
As a ninja of the hidden leaf village. You are going to get a task to retrieve a special scroll. But to prove that you are worthy to get that task. You need to solve a problem. You are given a BST and two keys which are the upper and lower limits of the range. The problem is to print BST keys in the given valid range. If you are able to print the key values. You’ll get the assignment.

Let’s better understand the problem statement by the following example.
Sample Example 🧐
Example 1:
Input: Range of keys are, key1: 14 and key2: 23.
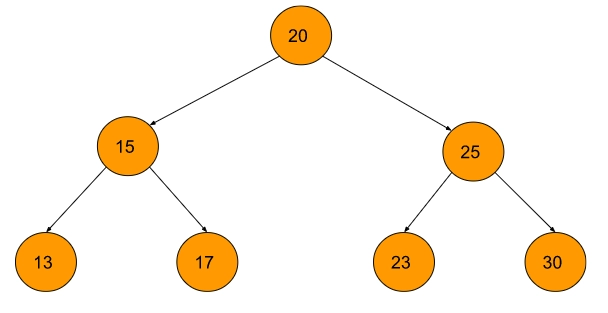
Output:
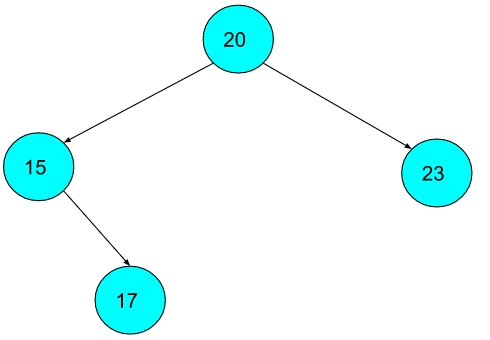
Explanation: The keys are 13, 15, 17, 20, 23, 25, 30
So keys in range 14 to 23 are 15, 17, 20, and 23.
Example 2:
Input: Range of keys are, key1: 8 and key2: 15.
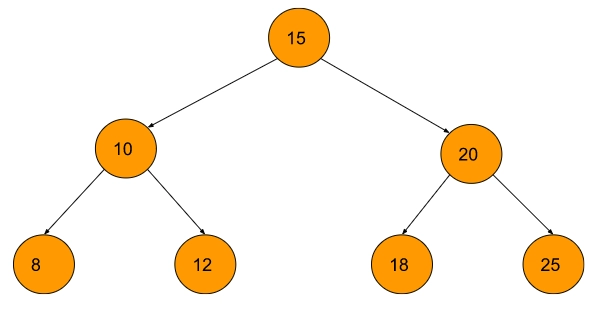
Output:
Explanation: The keys are 8, 10, 12, 15, 18, 20, 25
So keys in range 8 to 15 are 8, 12, 10, and 15.
In-Order Traversal Approach 🧑💻✨
We will use an in-order traversal approach to print BST keys in the given valid range. In this approach, when the tree is traversed in an in-order fashion. The keys are traversed in increasing order. So when we find that the key lies in the range, then we will print it. Otherwise, we will skip it.
Algorithm 🧑💻💫
-
Make a structure to store a BST node.
-
Now create a function to do the in-order traversal of the tree.
-
Now create a recursive function. It will take root as a parameter. And the range is (low, up)
- If the value of the root’s key is greater than low, then recursively call in the left subtree.
- If the value of the root’s key is in range, then print the root’s key.
-
Otherwise, recursively call the right subtree.
- Now modify the new tree accordingly.
Implementation 🧑💻🌝
#include<bits/stdc++.h>
#include <cmath>
#include<algorithm>
using namespace std;
#define FAST ios_base::sync_with_stdio(false); cin.tie(NULL);
//creating class Node
class Node
{
public:
int data;
Node *left;
Node *right;
};
//function to print values
//between low & up(low<up)
void Range(Node *root, int low, int Up)
{
if ( root==NULL )
return;
// traverse left subtree first
//If root->data > low, o/p the keys
if ( low < root->data )
Range(root->left, low, Up);
//similarly for data<=up
if ( low <= root->data && Up >= root->data )
cout<<root->data<<" ";
// traverse left subtree
Range(root->right, low, Up);
}
//----------------------------------Utility Function-----------------------------------//
Node* newNode(int data)
{
Node *temp = new Node();
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
//--------------------------------Main Function-------------------------------------//
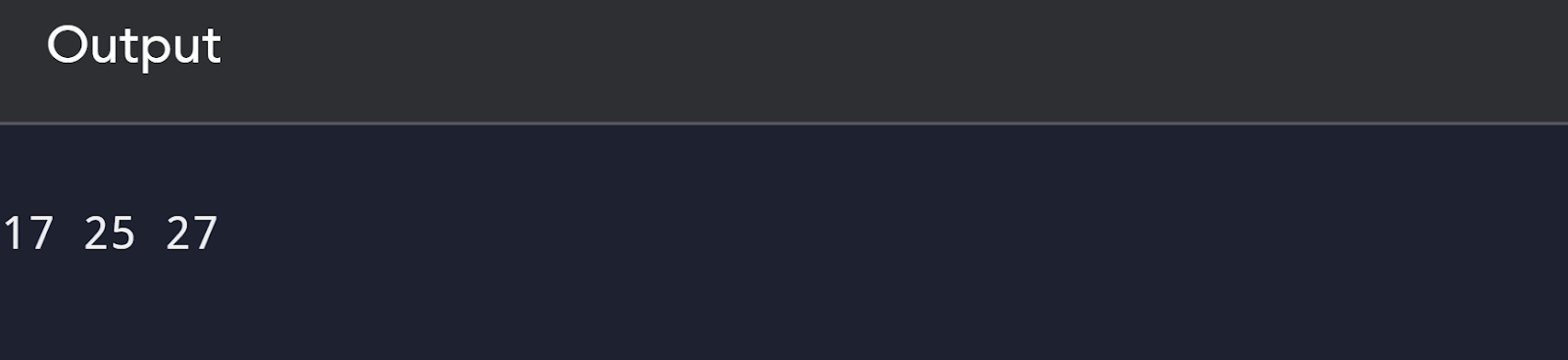
int main()
{
FAST;
Node *root = new Node();
int low = 15, Up = 30;
//value for tree construction
root = newNode(25);
root->left = newNode(13);
root->right = newNode(27);
root->left->left = newNode(9);
root->left->right = newNode(17);
Range(root, low,Up);
return 0;
}Output:
Time Complexity ⏳
The time complexity of the above approach is O(n). Here, n is the total number of keys in the tree. A single traversal on the tree is needed in this approach. That’s why time complexity is O(n).
Space Complexity 🌌
The space complexity O(h). Here, the “h” is the height of the tree. This approach will need space proportional to the tree's height for the recursive function call..