Introduction
Data structure and algorithms are one of the most important topics to understand if you want to prepare for a top product-based company. In this blog, we will take a quick look at the problem statement and discuss the recursion technique to solve the problem of printing the nodes at a k distance from the root. Here we are using the recursion to tackle the problem.
Problem Statement
Given a tree's root and integer k, print all nodes at a distance of k from the root.
Sample Examples
Example 1
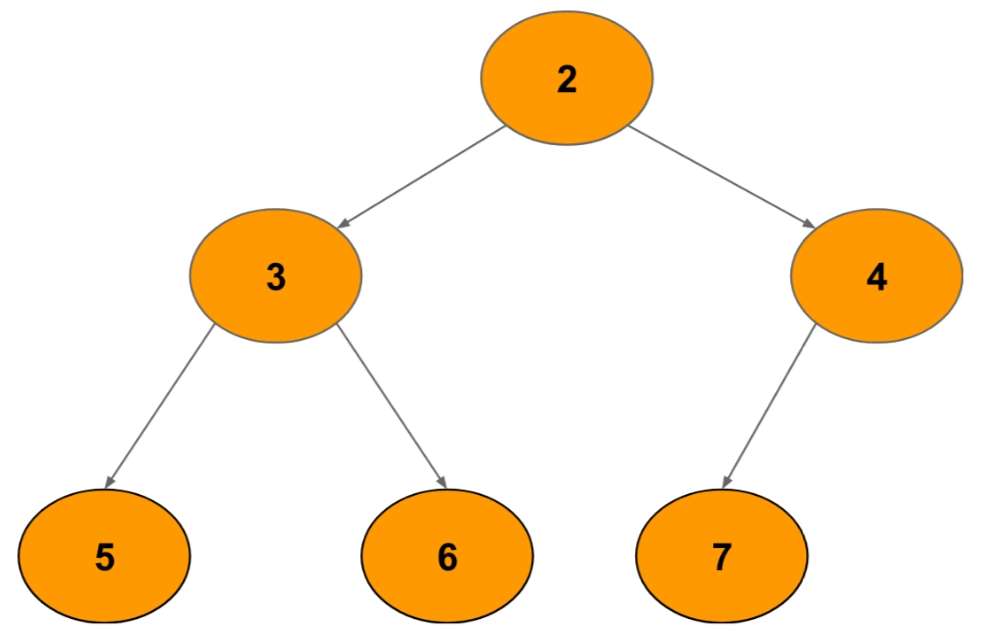
Input
Enter the K value: 1
Output
The Nodes are : 3 4
Explanation
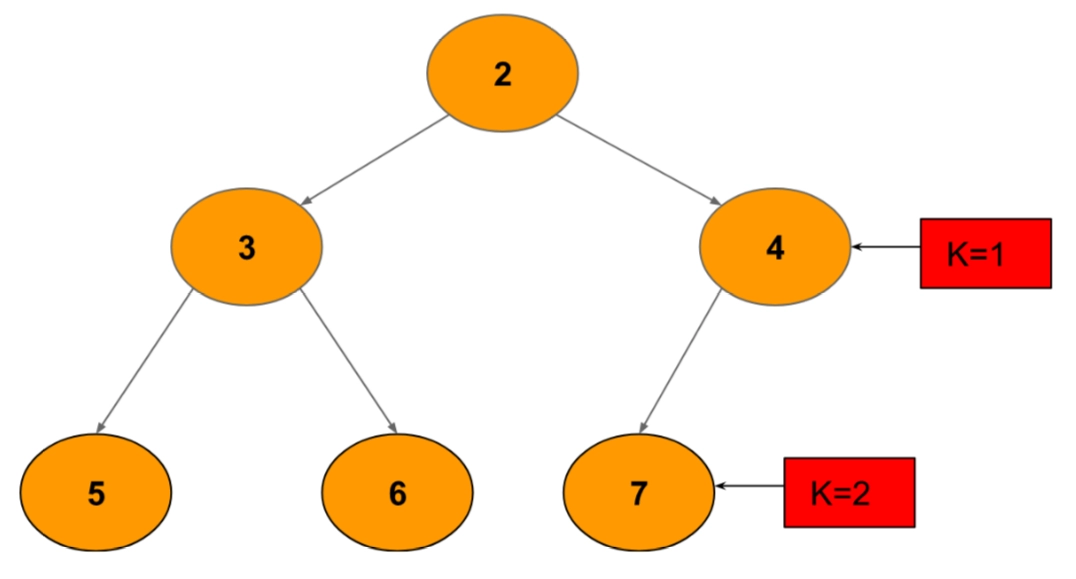
For K= 1, we have 3, 4 at distance 1.
Example 2
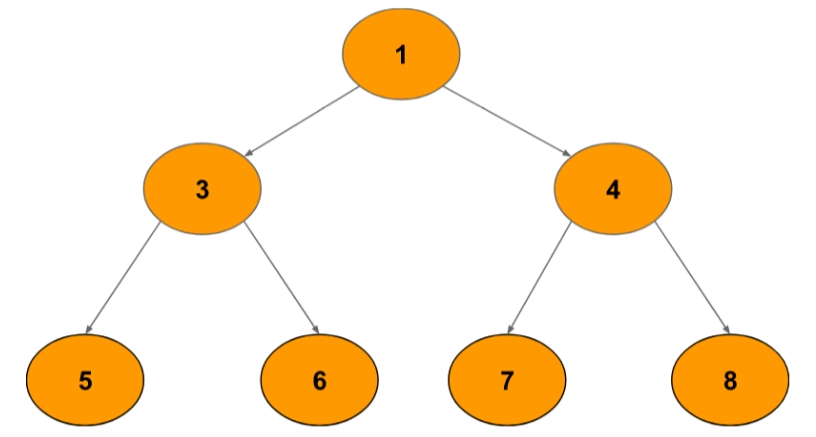
Input
Enter the K value: 2
Output
The Nodes are : 5 6 7 8
Explanation
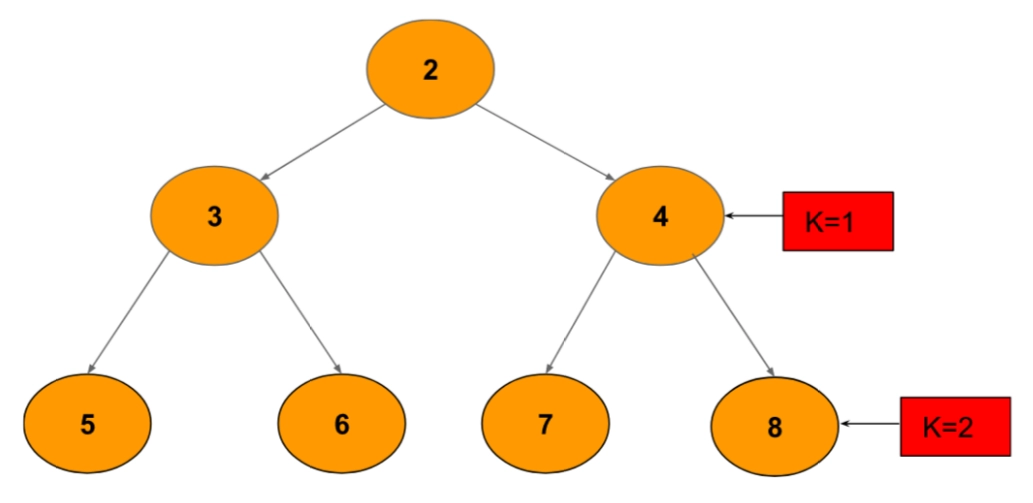
For K= 2, we have 5, 6, 7, and 8 at distance 2.
Recursive Approach
The method is straightforward: First, we accept the root node and k as input arguments to the function and check until k=0 is encountered. As soon as it is encountered, the value in the current node will be printed. Let's have a look at the algorithm and how it works.
Algorithm
-
Make a recursion function, let's say Klevel(node * root, int k).
-
With a distance of k-1, this function will recursively call itself in its left and right children.
- Finally, if k=0 is encountered, the value in the current node will be printed. The root will be k nodes away from this node.
Implementation in C++
#include<bits/stdc++.h>
using namespace std;
class Node
{
public:
int data;
Node* left, *right;
// allocates new node with data and NULL left,right pointers
Node(int data)
{
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
void Klevel(Node *Root , int k)
{
if(Root == NULL|| k < 0 )
return;
if( k == 0 )
{
cout << Root->data << " ";
return;
}
//left recursion
Klevel( Root->left, k - 1 ) ;
//right recursion
Klevel( Root->right, k - 1 ) ;
}
int main()
{
int k;
cout<<"Enter the K value: ";
cin>>k;
Node *root = new Node(2);
root->left = new Node(3);
root->right = new Node(4);
root->left->left = new Node(5);
root->left->right = new Node(6);
root->right->left = new Node(7);
cout<<"The Nodes are : ";
Klevel(root, k);
return 0;
}
Input
Enter the K value: 1
Output
The Nodes are : 3 4Time Complexity
Time complexity is O(n), where ‘n’ is the number of nodes in a binary tree.
Space Complexity
The space complexity will be O(height of the tree) as the maximum depth of the recursion stack can be the height of the tree.
Must Read Recursion in Data Structure




