Print Nodes between two given Level Numbers of a Binary Tree

Introduction

We'll take a quick look at the problem statement and discuss the level order tree traversal approach to solve the problem of printing the nodes between two given level numbers of a binary tree. Level Order traversal is one of the most famous binary tree traversal techniques which is also known as breadth-first traversal. There are different types of binary tree traversals - Inorder, Postorder, and Preorder. Please also have a look at this blog which explains the topic of Level Order Traversal in detail.

Problem Statement

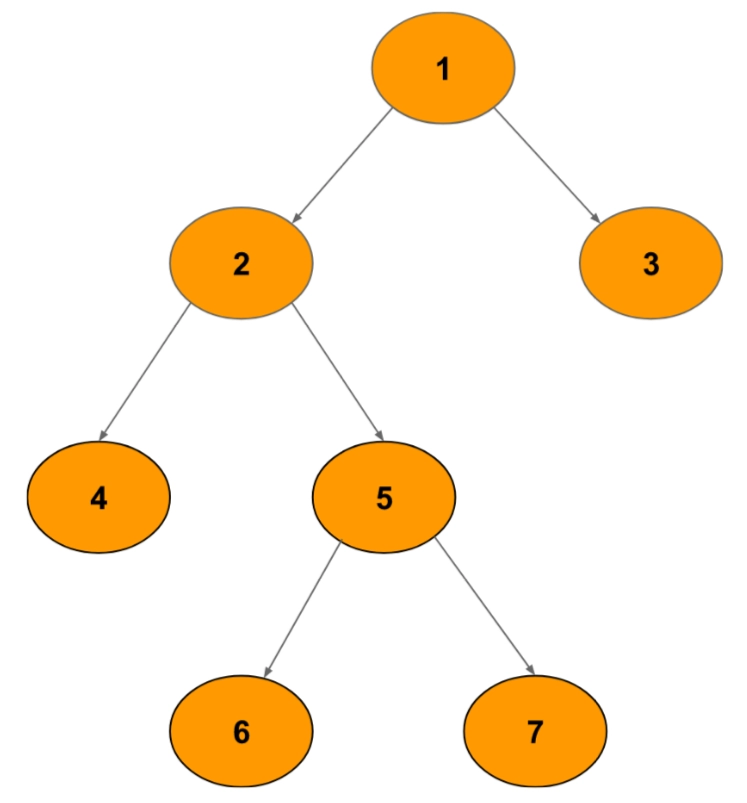
We are given a binary tree and two integers low and high, and we have to print the nodes from level low to level high (both inclusive).

Sample Examples

Input

Enter the low val: 2

Enter the high val: 3

Output

The nodes between given two levels is : 

2 3

4 5

Explanation

For low=2 and high=3 , we get the nodes 2, 3 at level 2 and 4, 5 at level 3. 

Approach

A straight approach would be to print all nodes of given levels one by one. Then call a recursive function using a loop from the upper level to the lower level in the tree. This algorithm is simple but more complex of order O(n^2), where n is the total number of nodes in the binary tree.

Using queue-based iterative level order traversal, we can print nodes in O(n) time. The goal is to perform a simple level order traversal using a queue. Add a marker node at the end of your inorder traversal. We raise the level number whenever we see a marker node. If the level number is between low and high, then print nodes.

Algorithm

1. Create a queue to store the tree node with level.
    
2. Push the root node into the queue with 1 as the level.
    
3. Do a level order traversal
   
   • Get the first element from the queue if it is in between low and high level and print it.
      
   • Push the left and right child of the node into the queue.
      
   • Keep repeating the above steps until our queue becomes empty.
      
4. Exit

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

struct Node
{
    int key;
    struct Node* left;
    struct Node* right;
};

//function to print node between low and high lvl
void lvl_order(Node* root, int low_val, int high_val)
{
    queue <Node *> q;
    int level = 1;
    
    // position node to indicate end of level
    Node *pos = new Node;

    // push only first level node and pos node for end of lvl
    q.push(root);
    q.push(pos);

    while (q.empty() == 0)
    {
        // Remove the front item from queue
        Node *n = q.front();
        q.pop();

        // Check if end of lvl is reached
        if (n == pos)
        {
            cout << endl;
            level++;  //increment lvl
            
            //if the queue is empty or lvl exceeds then break
            if (q.empty() == true || level > high_val) break;

            // Enqueue the pos for end of next level
            q.push(pos);
            continue;
        }
        //if level is above low print
        if (level >= low_val)
            cout << n->key << " ";

        // Enqueue the rest children
        if (n->left != NULL)
            q.push(n->left);
        if (n->right != NULL)
            q.push(n->right);
    }
}

// allocates new node with data and NULL left,right pointers
Node* newNode(int key)
{
    Node* temp = new Node;
    temp->key = key;
    temp->left = NULL;
    temp->right = NULL;
    return (temp);
}

int main()
{
    int low,high;
    cout<<"Enter the low val: ";
    cin>>low;
    cout<<"Enter the high val: ";
    cin>>high;
    struct Node *root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->left->right->left = newNode(6);
    root->left->right->right = newNode(7);

    cout << "The nodes between given two levels is : ";
    lvl_order(root, low, high);

    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Input

Enter the low val: 2
Enter the high val: 3

Output

The nodes between given two levels is : 
2 3
4 5

Time Complexity

Time complexity is O(n), where n is the number of nodes in a binary tree.

Space Complexity

A queue is used to store the node with its level. So, the space complexity of our program is O(n).