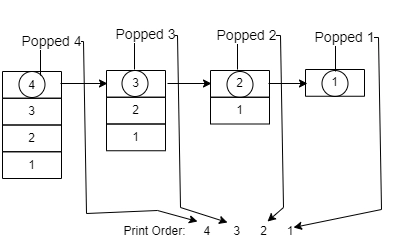
Approach 1: Array Stack
The first approach we will be using to solve this problem is array stack. Arrays are not dynamic in nature, but it is easy to implement.
- We will be creating an array for storing the stack elements.
- Push the top element from the stack to that array.
- Print the top element of the array stack.
- Pop out the element from the given stack.
- Repeat the above steps.
Implementation in Java
class Stack {
static final int MAX = 1000;
// Stores the index where element
// needs to be inserted
int top;
// Array stack
int arr[] = new int[MAX];
// Function to check whether array is empty or not
boolean isEmpty()
{
return (top < 0);
}
// Constructor
Stack() {
top = -1;
}
// Function that pushes the element
// to the top of the stack
boolean push(int s)
{
// If stack is full
if (top >= (MAX - 1)) {
System.out.println("Stack Overflow");
return false;
}
else {
arr[++top] = s;
return true;
}
}
// Function that removes the top
// element from the stack
int pop()
{
// If stack is empty
if (top < 0) {
System.out.println("Stack Underflow");
return 0;
}
else {
int s = arr[top--];
return s;
}
}
// To get the top element
int peek()
{
// If stack is empty
if (top < 0) {
System.out.println("Stack Underflow");
return 0;
}
else {
int s = arr[top];
return s;
}
}
// To print the elements of the stack
static void display(Stack s) {
// Create another stack
Stack s1 = new Stack();
// Until stack is empty
while (!s.isEmpty()) {
s1.push(s.peek());
// Print the element
System.out.print(s1.peek() + " ");
s.pop();
}
}
}
// Driver Code
class Main {
// Main function
public static void main(String args[])
{
Stack s = new Stack();
// Given stack
s.push(1);
s.push(2);
s.push(3);
s.push(4);
// Function Call
s.display(s);
}
}

You can also try this code with Online Java Compiler
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 100000
class Stack{
int top;
public:
Stack() {
top = -1;
}
// Array for storing the stack elements
int arr[MAX];
// Function to check if the stack is empty or not
bool isEmpty() {
return (top < 0);
}
// Function to pushes the element to the top
bool push(int x) {
if (top >= (MAX - 1)) {
cout << ("Stack Overflow\n");
return false;
}
// Insert the element x
else {
arr[++top] = x;
return true;
}
}
// Function to removes the top element
int pop() {
if (top < 0) {
cout << ("Stack Underflow\n");
return 0;
}
// Remove the element
else {
int x = arr[top--];
return x;
}
}
// Function for getting the top element
int peek() {
if (top < 0) {
cout << ("Stack Underflow\n");
return 0;
}
// Reading the top element
else {
int x = arr[top];
return x;
}
}
// Function to print and restore the stack
void DisplayStack(Stack s) {
Stack s1;
while (!s.isEmpty()) {
s1.push(s.peek());
// Print the elements
cout << (s1.peek()) << " ";
s.pop();
}
}
};
// Driver Code
int main()
{
Stack s;
// The given stack
s.push(1);
s.push(2);
s.push(3);
s.push(4);
s.DisplayStack(s);
}

You can also try this code with Online C++ Compiler
Implementation in Python
MAX = 1000
# Pointer to th top of stack
top = -1
# Empty Array for storing elements
a = [0]*MAX
# Function to check
# if stack is empty or not
def isEmpty():
return (top >= 0)
# Function that pushes the element to the top of the stack
def push(x):
global top
# Check if stack is full
if (top >= (MAX - 1)):
print("Stack Overflow")
return False
# Otherwise insert the element x
else:
top+=1
a[top] = x
return True
# Function that removes the top element from the stack
def pop():
global top
# If stack is empty
if (top < 0):
print("Stack Underflow")
return 0
# Otherwise remove element
else:
top-=1
x = a[top]
return x
# Function to get the top element
def peek():
# If stack is empty
if (top < 0):
print("Stack Underflow")
return 0
# Otherwise remove element
else:
x = a[top]
return x
# Function to print the elements
# and restore the stack
def DisplayStack():
# Until stack is empty
x = peek()
while (x):
# Print the element
print(x, end = " ")
x = pop()
# Given stack
push(1)
push(2)
push(3)
push(4)
# Function Call
DisplayStack()

You can also try this code with Online Python Compiler
Output
4 3 2 1
Complexity Analysis
Time Complexity: O(n), n=number of elements.
Space Complexity: O(n).
Must Read Difference between ArrayList and LinkedList
Approach 2: Recursive
We will use a function that will be recursive(see Recursion) and print the elements of the stack from top to bottom.
- Declare a recursive function.
- Add a base condition to it; if the stack is empty, print return.
- Declare a variable that will store the top element and remove that element from the stack.
- Print the value of the variable and call the recursive function.
- Push that variable back into the stack to restore the stack as it was.
Implementation in JAVA
import java.util.*;
class Solution{
// To print the elements of the stack
public static void Print(Stack<Integer> s)
{
// If stack is empty
// Base condition
if (s.empty())
return;
// To store the top element of the stack
int t = s.peek();
// Pop the top element
s.pop();
// Print the variable 't'
System.out.print(t + " ");
// Print the remaining stack
PrintStack(s);
// Push the element back to restore the stack
s.push(t);
}
// Main function
public static void main(String[] args)
{
Stack<Integer> s = new Stack<Integer>();
// Given stack s
s.push(1);
s.push(2);
s.push(3);
s.push(4);
// Recursive Function call
Print(s);
}
}

You can also try this code with Online Java Compiler
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
// Function to print elements from top to bottom
void PrintStack(stack<int> s)
{
// If stack is empty
if (s.empty())
return;
// Get the top of the stack
int x = s.top();
// Pop the top element
s.pop();
// Print the current top of the stack i.e., x
cout << x << ' ';
// Recursive Call
PrintStack(s);
// Push the element back
s.push(x);
}
// Driver Code
int main()
{
stack<int> s;
// The given stack s
s.push(1);
s.push(2);
s.push(3);
s.push(4);
// Function Call
PrintStack(s);
return 0;
}

You can also try this code with Online C++ Compiler
Implementation in Python
from queue import LifoQueue
# Function to print stack elements from top to bottom with the order of elements unaltered
def PrintStack(s):
# Check if stack is empty
if (s.empty()):
return;
# Extract the top
x = s.get();
# Remove the top element
#s.pop();
# Print current top
# of the stack i.e., x
print(x, end = " ");
# Recurse to print
# remaining stack
PrintStack(s);
# Push the element
# back
s.put(x);
# Driver code
if __name__ == '__main__':
s = LifoQueue();
# Given stack s
s.put(1);
s.put(2);
s.put(3);
s.put(4);
# Function call
PrintStack(s);

You can also try this code with Online Python Compiler
Output
4 3 2 1
Complexity Analysis
Time Complexity: O(n), n=number of elements
Space Complexity: O(n).
Must Read Stack Operations
Frequently Asked Questions
What do you mean by Stack data structure?
Stack is a linear data structure to store elements in order. It follows the LIFO principle(Last In First Out), which prints the last element inserted in the stack as the first element.
How many approaches are there to print elements of the stack from top to bottom?
There are three approaches to solving this problem:
- Array Stack
- Recursive
- Singly LinkedList
What is the time complexity of the recursive approach?
Time Complexity is O(n), where n is the number of elements in the stack.
Conclusion
In this blog, we talked about stacks and, most importantly, how to print the elements from top to bottom such that elements are present in the stack without their order being changed. We have implemented the problem using two approaches in C++, Java, and Python.
Building the foundation of any topic is necessary, so first, you should gain more knowledge on Stacks before heading into its problems.
You can also consider our Mern Stack Course to give your career an edge over others.
Happy Coding!