Introduction
A tree data structure is a hierarchical data structure organized in a tree-like shape. It is made up of a core node, structural nodes, and sub-nodes that are linked together via edges. The roots, branches, and leaves of a tree data structure are all related to one another. Binary Tree: A Binary tree is one in which each node has precisely zero or two children. A perfect binary tree is one in which each node, except leaf nodes, has a degree of two. In this blog, we discuss the problem of printing the nodes at odd levels of a tree. We here consider a binary tree, and the level of the root node is 1.
Problem Statement
In this blog, we discuss the problem of printing the nodes at odd levels of a binary tree.
Sample Example
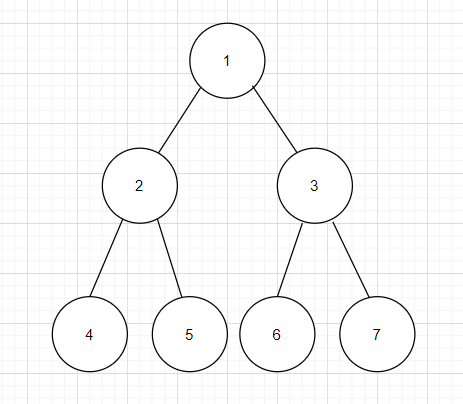
Output: 1 4 5 6 7
Explanation: The above-printed elements correspond to levels one and 3rd, which are odd levels.
Recursive Approach
The first approach involves using recursion. Below is the mentioned algorithm:
- We simply do the preorder traversal of the binary tree.
- Maintain a variable level. When calling for a successor node, increment the level by 1.
- If the level is odd, print the node value.
Pseudocode
Preorder(root, level):
If root is Null:
Return
If level is odd:
print(root->value)
Preorder(root->left, level+1)
Preorder(root->right, level+1)Implementation in C++
#include "bits/stdc++.h"
using namespace std;
// Class for defining a Tree Node;
class Node{
public:
int value;
Node* left;
Node* right;
};
// Function to construct a new Node;
Node* NewNode(int val){
Node* node = new Node;
node->value = val;
node->left = NULL;
node->right = NULL;
return node;
}
//To check if a leaf node;
bool leaf(Node* root){
return(!root->left && !root->right);
}
void printOddLevel(Node* root, int level){
if(!root){
return;
}
// If odd level, print the node value;
if(level%2){
cout<<root->value<<" ";
}
printOddLevel(root->left, level+1);
printOddLevel(root->right, level+1);
}
void solve()
{
Node* root = NewNode(1);
root->left = NewNode(2);
root->right = NewNode(3);
root->left->left = NewNode(4);
root->left->right = NewNode(5);
root->right->left = NewNode(6);
root->right->right = NewNode(7);
// root->right->right->right = NewNode(8);
int level = 1;
cout<<"Odd level Nodes: ";
// Function for printing the nodes;
printOddLevel(root, level);
}
int main()
{
solve();
return 0;
}Implementation in Python
#Defining the class node
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def PrintOddLevel(root, level):
if root == None:
return
#Print if odd level node
if level%2:
print(root.data, end = " ")
#Recursive call for left child of root
PrintOddLevel(root.left, level+1)
#Recursive call for right child of root
PrintOddLevel(root.right, level+1)
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
#Function For printing odd level nodes
PrintOddLevel(root, 1)
Output:
1 4 5 6 7
Complexity Analysis
Time complexity: O(n)
Explanation: As we traverse each node once, therefore the Time complexity of the above approach is O(n), where n denotes the number of nodes in the Tree.
Space complexity: O(n)
Explanation: Here, we see the maximum depth of the recursive stack is the corresponding space complexity. Therefore, the space complexity is O(n).
Must Read Recursion in Data Structure





