Introduction
A BST (Binary Search Tree) is a tree in which the key of the nodes of the left sub-tree has a lower value than its parent node's key. And the key of the right sub-tree is greater than or equal to the key of its parent (root) node.
A binary Search Tree is a collection of nodes that are arranged in such a way that they retain BST properties.
In this article, we will solve a question based on the topic of BST. The question says to print the sum of k smallest elements in BST.
Problem Statement
In this question, the goal is to determine the sum of all elements that are less than or equal to Kth's smallest element.
Let's take some examples of the given problem statement.
Sample Examples
Example 1:
Input:
k = 3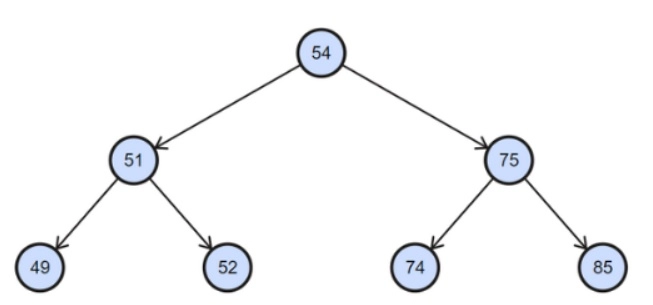
Output:
152
Example 2:
Input:
k = 3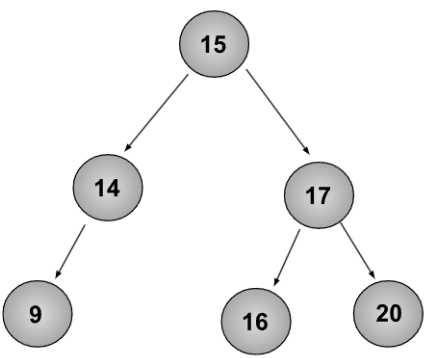
Output:
38Naive Approach
The most basic pattern search algorithm is known as naive pattern searching. It checks that each character in the primary string matches the pattern. For a specific type of pattern question, this algorithm is useful. No pre-processing steps are required in this approach.
Let's now discuss the algorithm for the above approach.
Algorithm to print the sum of k smallest elements in BST
🚩 Perform the Inorder traversal to the given BST.
🚩 Count the number of elements visited.
🚩 Add all the elements to an integer variable.
🚩 Return the integer variable when the count of the element is equal to k.
Implementation
C++
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int data;
Node *left, *right;
};
struct Node *
createNode (int data)
{
Node *new_Node = new Node;
new_Node->left = NULL;
new_Node->right = NULL;
new_Node->data = data;
return new_Node;
}
struct Node *
insert (Node * root, int key)
{
if (root == NULL)
return createNode (key);
if (root->data > key)
root->left = insert (root->left, key);
else if (root->data < key)
root->right = insert (root->right, key);
return root;
}
int ksmallestSum (Node * root, int k, int &count)
{
if (root == NULL)
return 0;
if (count > k)
return 0;
int res = ksmallestSum (root->left, k, count);
if (count >= k)
return res;
res += root->data;
count++;
if (count == k)
return res;
return res + ksmallestSum (root->right, k, count);
}
int ksmallestSum (struct Node *root, int k)
{
int count = 0;
return ksmallestSum (root, k, count);
}
int main ()
{
Node *root = NULL;
root = insert (root, 49);
root = insert (root, 46);
root = insert (root, 44);
root = insert (root, 47);
root = insert (root, 70);
root = insert (root, 69);
root = insert (root, 80);
int k = 3;
cout << "Sum of k smallest elements is " << ksmallestSum (root, k) << endl;
return 0;
}
Output:
Sum of k smallest elements is 137Time Complexity
The time complexity of the above code is O(N) (where N is the number of elements in the tree). We have gone through the complete tree to perform the Inorder traversal.
Space Complexity
The space complexity of the above code is O(1). It is O(1) because the integer variable takes one extra space in the memory.
Read More - Time Complexity of Sorting Algorithms




