Introduction
Here in this blog, we are asked to see various approaches to find the product of the maximum element of the first array and the minimum element of the second array. We are already familiar with the array data structures and their various operations. So, let's delve a little deeper into this blog.

Source: DSA
Problem Statement
In this problem, we are given two arrays of different lengths or maybe the same length. And we are asked to find the product of the maximum element of the first array and the minimum element of the second array. The problem statement is straightforward and simple; find the maximum element of the first array then find the minimum element of the second array and finally multiply both the elements. We can try different approaches to solve this problem. Let us understand the problem statement with the help of an example.
Sample Example
Assume that the first array nums1 is: {2,3,4,5,6} and second array nums2 is: {3,6,8,9,5}.
As we can see from the array that the maximum element in nums1 is 6 and the minimum element in the second array is 3. After multiplying both the elements, we get the answer as 6 * 3 = 18.
The problem statement is quite clear with the above example.
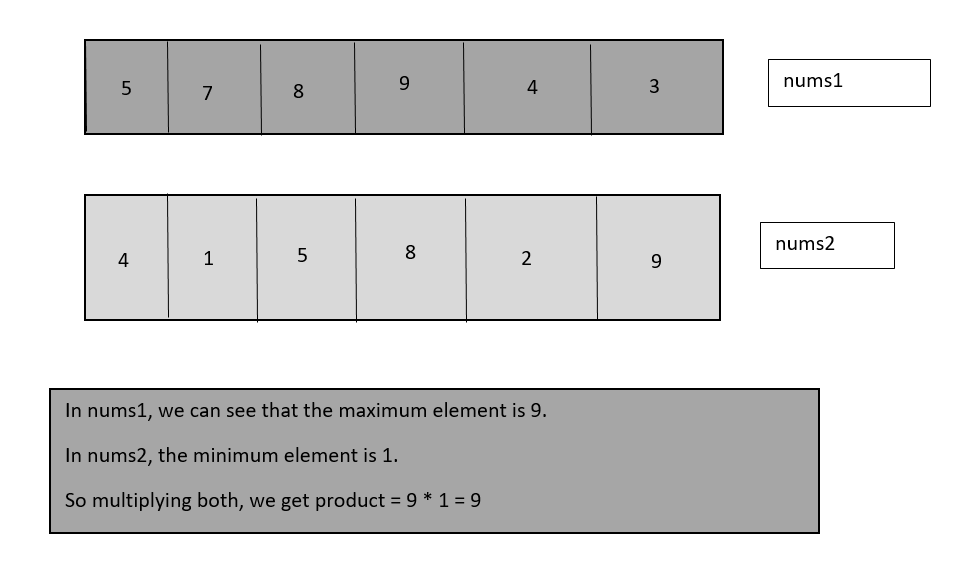
In the above diagram, we can clearly see that the maximum element from the first array is 9 and the minimum element from the second array is 1. And we have to multiply both the numbers. So the result is 9.
Recommended topic, kth largest element in an array and Euclid GCD Algorithm
Approach 1: Naive approach
This approach is very simple to implement and straightforward. In this approach, we will first sort both arrays in ascending order. And after sorting the arrays, we already have an idea that in the first array, the maximum element will be at the last index, and for the second array, the minimum element will be at the first index. We simply have to return the products of both the index’s elements.

Source: Naive approach
Let us see its algorithm.
Steps of Algorithm
Step 1: Sort both the arrays in ascending order using the inbuilt sort function or user-defined functions.
Step 2: After sorting both arrays, multiply the last element of nums1 i.e. the maximum element, and the first element of nums2 i.e. the minimum element.
Step 3: Return the multiply as the result. Let us see a diagram to understand this algorithm.
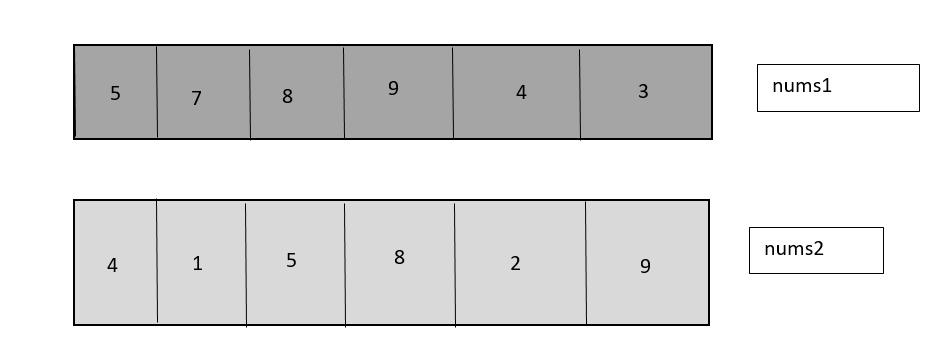

Let us see the implementation of this approach in the next section of this blog.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
int MinMaxProduct(int nums1[],
int nums2[],
int n1,
int n2)
{
sort(nums1, nums1 + n1); //sorting the arrays
sort(nums2, nums2 + n2);
return nums1[n1 - 1] * nums2[0]; // Return product of maximum and minimum elements.
}
int main()
{
int nums1[100], nums2[100], n1, n2;
cout << "Enter Number of elements in array 1: ";
cin >> n1;
cout << "Enter element "<<endl;
for (int i = 0; i < n1; i++) {
cin >> nums1[i];
}
cout << "Enter Number of elements in array 2: ";
cin >> n2;
cout << "Enter element " <<endl;
for (int i = 0; i < n2; i++) {
cin >> nums2[i];
}
cout << "result of maximum and minimum elements is: "<<MinMaxProduct(nums1, nums2, n1, n2);
return 0;
}
Output:
Enter Number of elements in array 1: 4
Enter element
2 5 8 0
Enter Number of elements in array 2: 4
Enter element
2 0 1 5
result of maximum and minimum elements is: 0Implementation in Java
import java.util.*;
public class MinMaxProduct {
public static int Product(int nums1[], int nums2[], int n, int m) {
Arrays.sort(nums1); //inbuilt function to sort both the arrays
Arrays.sort(nums2);
return nums1[n - 1] * nums2[0]; //product of both the maximum and minimum elements
}
public static void main(String argc[]) {
int[] nums1 = new int[] {5,7,8,9,4,3};
int[] nums2 = new int[] {4,1,5,8,2,9};
int n = 6;
int m = 6;
System.out.println("product of maximum and minimum elements is: " + Product(nums1, nums2, n, m));
}
}
Output:
product of maximum and minimum elements is: 9
Let us analyze the time and complexity of this approach.
Complexity analysis
Time complexity
This approach will take O(n log n ). Because in this approach, we are using the concept of sorting the array first in ascending order and returning the product of maximum and minimum elements of the arrays.
Space complexity
This will not cost any memory space. And it will take O(1).





