Program to Check Idempotent Matrix

Test Cases

Following are the test cases,

Test Case1

Input 

{
{2, -1, -3},
{-1, 2, 3},
{1, -1, -2}
}

Output

Idempotent Matrix

Explanation

Below is the explanation,

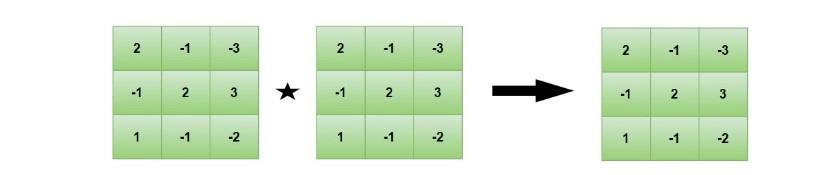
For the matrix

{

{2, -1, -3},

{-1, 2, 3},

{1, -1, -2}

}

After multiplying with itself, we are getting the same matrix back, as shown below. 

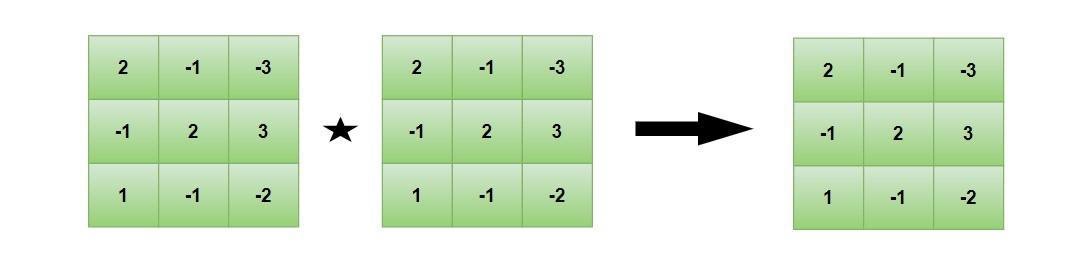
So it is an Idempotent Matrix.

Test Case2

Input 

{
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
}

Output

Not Idempotent Matrix

Explanation

{

{1, 2, 3},

{4, 5, 6},

{7, 8, 9}

}

After multiplying with itself, we are getting the same matrix back, as shown below. 

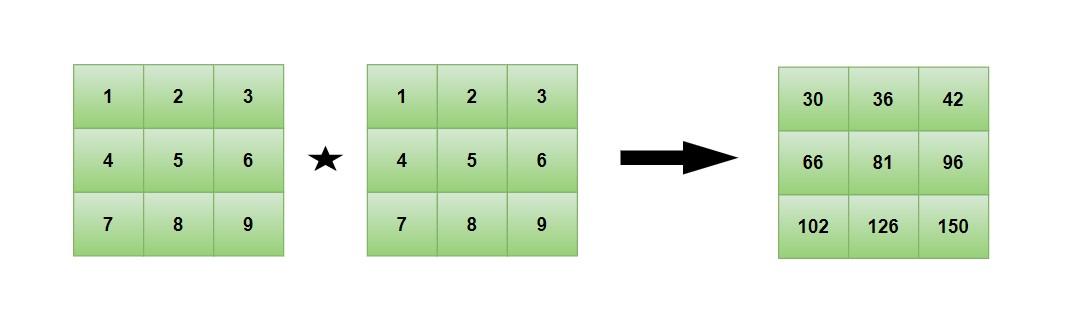
So it is Not an Idempotent Matrix.

Solution

The solution is shown below,

Algorithm

• Take the matrix in a 2D array.
• Multiply the matrix with itself and store the result in another matrix.
• Then, check whether the initial and result matrix is the same.
• If they are the same, then the matrix is idempotent. Otherwise, not.

Implementation

Here in this section, we will implement the above algorithm in different languages.

C++ Code

#include<bits/stdc++.h>
using namespace std;

#define n 3

// function to check for idempotent matrix
bool is_idempotent(int matrix[][n]) {
    // stores the multiplication result
    int result[n][n];

    // matrix multiplication
     for(int i = 0; i < n ; i++) {
        for(int j = 0 ; j < n ; j++) {
            result[i][j] = 0;
            for(int k = 0; k < n ; k++) {
                result[i][j] += (matrix[i][k] * matrix[k][j]);
            }
        }
    }

    // check whether we are getting same matrix after performing multiplication
    for(int i = 0; i < n ; i++) {
        for(int j = 0; j < n ; j++) {
            if(matrix[i][j] != result[i][j])  return false;
        }
    }

    return true;
}

int main()
{
     int matrix[n][n] = {{2, -1, -3} , {-1, 2, 3} , {1, -1, -2}};
    if(is_idempotent(matrix)) {
        cout << "Idempotent Matrix";
    }
    else{
        cout << "Not Idempotent Matrix";
    }
   
    return 0;

}

You can also try this code with Online C++ Compiler

Run Code

Java Code

class Main{
    static int n = 3;
    static boolean is_idempotent(int matrix[][]) {
        // stores the multiplication result
        int[][] result= new int[n][n];
   
        // matrix multiplication
         for(int i = 0; i < n ; i++) {
            for(int j = 0 ; j < n ; j++) {
                result[i][j] = 0;
                for(int k = 0; k < n ; k++) {
                    result[i][j] += (matrix[i][k] * matrix[k][j]);
                }
            }
        }
   
        // check whether we are getting same matrix after performing multiplication
        for(int i = 0; i < n ; i++) {
            for(int j = 0; j < n ; j++) {
                if(matrix[i][j] != result[i][j])  return false;
            }
        }
   
        return true;
    }
   
    public static void main(String[] args) {
        // given matrix
        int[][] matrix = {{2, -1, -3} , {-1, 2, 3} , {1, -1, -2}};

        // check for idempotent matrix
         if(is_idempotent(matrix)) {
             System.out.print("Idempotent Matrix");
         }
         else{
             System.out.print("Not Idempotent Matrix");
         }
       
    }
}

You can also try this code with Online Java Compiler

Run Code

Python Code

def is_idempotent(matrix):
    # result matrix

    n = len(matrix)

    # store the result
    result = [[0] * n for i in range(0 , n)]

    # multipying the matrix with itself
    for i in range(0 , n):
        for j in range(0 , n):
           # print(matrix[i][j], end=' ')
            result[i][j] = 0
            for k in range(0 , n):
                result[i][j] += (matrix[i][k] * matrix[k][j])

    # check for equality
    for i in range(n):
        for j in range(n):
            if matrix[i][j] != result[i][j]:
                return False
    return True


matrix = [[2 , -1, -3],
          [-1, 2, 3],
          [1, -1, -2]]

if (is_idempotent(matrix)):
    print("Idempotent Matrix")
else:
    print("Not Idempotent Matrix")

You can also try this code with Online Python Compiler

Run Code

Output

Idempotent Matrix

Complexity Analysis

Time Complexity: O(n²)

Space Complexity: O(n²)

Frequently Asked Questions

What are the ways we can traverse a matrix?

There are mainly two ways to traverse a matrix:

• Row-wise traversal(Row-major Traversal)
• Column-wise traversal(Column-major Traversal)
   

Is Identity Matrix Idempotent Matrix?

We know that for Identity Matrix I, if we multiply the matrix by itself, it returns the same matrix, i.e. I² = I, so Identity Matrix is Idempotent.
 

Is Null or Zero Matrix Idemoptent Matrix?

Null or Zero Matrix is an Idempotent Matrix. As When multiplying with itself, it returns the same matrix.
 

What are the time and space complexity of traversing a matrix of size NxN?

Time Complexity: O(N²)

Space Complexity: O(1)

Conclusion

In this article, we have discussed the Program to Check Idempotent Matrix.

We started with the basic introduction, then we discussed,

• Problem Statement
• What Idempotent Matrix is
• Solution 
  • Algorithm to follow
  • Implementation of the algorithm in C++, Java, Python
  • Complexity Analysis

We hope you have some idea from this article regarding the Program to Check Idempotent Matrix.

To learn more, follow our articles on Transpose of a Matrix in C, Book Allocation Problem, Getch in C and Matrix in Zig-Zag Form.

Please upvote this article to help other Ninjas grow.

Explore our practice platform Coding Ninjas Studio to practice top problems, attempt mock tests, read interview experiences, interview bundle, follow guided paths for placement preparations, and much more.!

Happy Reading!