Algorithm
Start
Step 1 -> define macro as #define size 3
Step 2 -> declare function for matrix multiplication.
void multiplyMatrix(int arr[][size], int res[][size])
Loop For int i = 0 and i < size and i++
Loop For int j = 0 and j < size and j++
Set res[i][j] = 0
Loop For int k = 0 and k < size and k++
res[i][j] = res[i][j] +( arr[i][k] * arr[k][j])
End
End
End
Step 3 -> declare function to check involutory matrix or not
bool check(int arr[size][size])
declare int res[size][size]
Call multiply(arr, res)
Loop For int i = 0 and i < size and i++
Loop For int j = 0 and j < size and j++
IF (i == j && res[i][j] != 1)
return false
End
If (i != j && res[i][j] != 0)
return false
End
End
End
Return true
Step 4 -> In main()
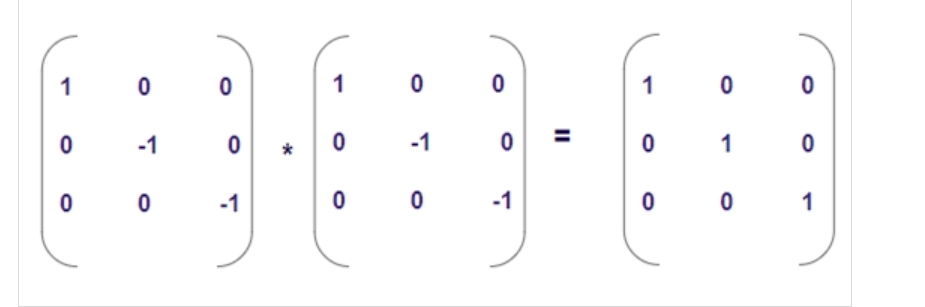
Declare a matrix int arr[size][size] = { { 1, 0, 0 },
{ 0, -1, 0 },
{ 0, 0, -1 } }
If (check(arr))
Print its an involutory matrix
Else
Print its not an involutory matrix
Stop
Program
Now we are going to see programs to Check Involutory Matrix. We will implement it in C++ and Java language by using the algorithm mentioned above. Below is the program to Check Involutory Matrix is as follows:
C++ Code
// Program to check involutory matrix.
#include <bits/stdc++.h>
#define N 3
using namespace std;
// Function to multiply matrix
void multiply(int mat[][N], int mult[][N])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
mult[i][j] = 0;
for (int k = 0; k < N; k++)
mult[i][j] += mat[i][k] * mat[k][j];
}
}
}
// Function to check involutory matrix.
bool InvolutoryMatrix(int mat[N][N])
{
int res[N][N];
// multiply function call.
multiply(mat, res);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (i == j && res[i][j] != 1)
return false;
if (i != j && res[i][j] != 0)
return false;
}
}
return true;
}
// Driver function.
int main()
{
int mat[N][N] = { { 1, 0, 0 },
{ 0, -1, 0 },
{ 0, 0, -1 } };
// Function call. If function return
// true then if part will execute otherwise
// else part will execute.
if (InvolutoryMatrix(mat))
cout << "Given matrix is an involutory Matrix";
else
cout << "Given matrix is not an involutory Matrix";
return 0;
}

You can also try this code with Online C++ Compiler
Output
Given matrix is an involutory Matrix

You can also try this code with Online C++ Compiler
Java Code
// Java Program to implement
// involutory matrix.
import java.io.*;
class CodingNinjas {
static int N = 3;
// Function for matrix multiplication.
static void multiply(int mat[][], int res[][])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
res[i][j] = 0;
for (int k = 0; k < N; k++)
res[i][j] += mat[i][k] * mat[k][j];
}
}
}
// Function to check involutory matrix.
static boolean InvolutoryMatrix(int mat[][])
{
int res[][] = new int[N][N];
// multiply function call.
multiply(mat, res);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (i == j && res[i][j] != 1)
return false;
if (i != j && res[i][j] != 0)
return false;
}
}
return true;
}
// Driver function.
public static void main (String[] args)
{
int mat[][] = { { 1, 0, 0 },
{ 0, -1, 0 },
{ 0, 0, -1 } };
// Function call. If function return
// true then if part will execute
// otherwise else part will execute.
if (InvolutoryMatrix(mat))
System.out.println ( "Given matrix is an involutory Matrix");
else
System.out.println ( "Given matrix is not an involutory Matrix");
}
}

You can also try this code with Online Java Compiler
Output
Given matrix is an involutory Matrix

You can also try this code with Online Java Compiler
Time Complexity: Time complexity is O(n3) where n is the size of the square matrix.
Also see, Rabin Karp Algorithm
Frequently Asked Questions
Is it possible to tell if a matrix is idempotent?
If and only if the matrix 'M' multiplied by itself returns the same matrix 'M,' i.e. M * M = M, a matrix 'M' is called an idempotent matrix.
Is it true that the matrix is orthogonal?
If the transpose of a square matrix with real numbers or elements equals the inverse matrix, the matrix is said to be orthogonal.
Is it true that a null matrix is nilpotent?
A nilpotent matrix is a square matrix in which the product of the matrix and itself is a null matrix.
What is the involutory matrix's inverse?
An involutory matrix is a square matrix that is its own inverse in mathematics. That is, if and only if A^2 = I, where I is the n*n identity matrix, multiplication by the matrix A is an involution.
Conclusion
This article extensively discussed how to check whether a matrix is an involutory matrix or not.
We hope you have learned something new from this blog. And if you're interested in learning more, see our posts on Operations On Matrices, Construct a Linked List from a 2D Matrix, Matrix Chain Multiplication, Types of Matrix. Please vote for our blog to help other ninjas succeed.
Visit our practice platform Coding Ninjas Studio to practice top problems, attempt mock tests, read interview experiences, and much more.!
Happy Reading!