Program to find the number of misplaced elements from the index after sorting

Introduction

Problem statement

We are given an array having n elements. After Sorting the given array, our task is to count the number of misplaced elements from the index.

Sample Examples

Example 1:

Input: a[] = { 6, 2, 3, 8, 9 ,1 }
Output:  4
Explanation
Sorted array = { 1, 2, 3, 6, 8, 9 }
Index of elements {1, 6, 8, 9} are misplaced after sorting

Example 2:

Input: a[]={7, 5, 9, 3, 4}
Output:  5
Explanation
Sorted array = {3, 4, 5, 7, 9}
All elements are misplaced from their indexes.

Approach

The idea is simple, sort the given array and store it in a temporary array. Now compare all the elements of the given array from the corresponding elements of the temporary array (sorted). If the corresponding elements are not the same, count and store them in a count variable.

After comparing all the elements, return the value of the count.

Steps of algorithm

• Create a temporary array of size same as the given array, temp[n].
• Store all the elements of the given array in the temporary array.
• Sort the temporary array using the sort function, sort(temp, temp+n).
• Create a count variable and initialize it with 0, count = 0.
• Compare the elements of the given array with the elements in the temporary array. If the elements are not the same, increment the count variable by 1 (count++).
• Finally, return the value of the count.

Let’s understand the above steps with an example:

• Copy all the elements in the temp array.
   

• Sort the temp array, sort(temp, temp+n)
   

• Compare the elements.
   

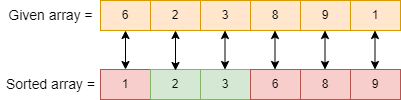
                        Misplaced elements are {1, 6, 8, 9} 

                         count = 4

• Return the value of the count.
   

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

int count_misplaced(int a[], int n)
{
  int temp[n];

  for (int i = 0; i < n; i++)
  {
    temp[i] = a[i];
  }

  sort(temp, temp + n);

  int count = 0;

  for (int i = 0; i < n; i++)
  {
    if (temp[i] != a[i])
      count++;
  }

  return count;
}

int main()
{
  int a[] = {6, 2, 3, 8, 9 , 1};

  int n = sizeof(a) / sizeof(a[0]);

  cout << " Number of misplaced elements: " << count_misplaced(a, n);
  
  return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output:

Number of misplaced elements: 4

You can also try this code with Online C++ Compiler

Run Code

Complexity Anlaysis

Time complexity: We are using a sort function to sort the temporary array, so the time complexity is O(n*logn).

Space complexity: O(n), as we are using a temporary array (temp).

Also see,  Rabin Karp Algorithm.