Properties of Minimum Spanning Tree (MST)

Introduction

Spanning Tree: For a connected and undirected graph, a spanning tree is a subgraph and a subset of the edges of the main graph that doesn’t have cycles and connects all the vertices. A connected and undirected graph will have at least one spanning tree. For an in-depth knowledge of graphs, check out this course.

Minimum Spanning Tree: For a connected, weighted, and undirected graph, a Minimum Spanning Tree(MST) or also called a minimum weight spanning tree, is a spanning tree with a weight less than or equal to the weight of all other spanning trees. The weight of a spanning tree is the sum of the weights of its edges.

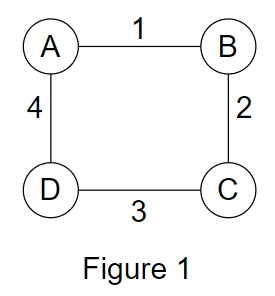
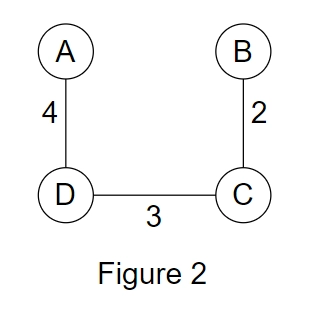
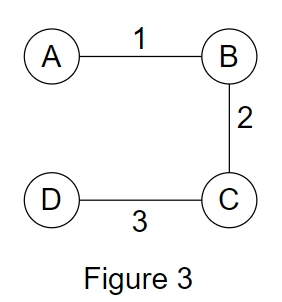
E.g., In the figures given below:

Figure1: Given connected and undirected graph G.

Figure2: One of the Spanning trees of graph G.

Figure3: Minimum spanning tree(MST) of graph G.

Let’s discuss the properties of MST.

Alert Ninjas:  Don’t stop now! Enroll in the Competitive Programming course today and start coding. Learn the art of writing time and space-efficient code and compete in code competitions worldwide. 

Also, check out the Minimum Spanning Tree Problem.

Properties

Multiplicity

There can be a case of more than one minimum spanning tree. Consider a connected and undirected graph G(V, E) where V is the number of vertices and E is the number of edges in graph G.

A spanning tree always contains V-1 edges(as the minimum number of edges required to connect V vertices is V-1). Therefore, E-V+1 edges are not part of the spanning tree. It is possible to use some of these edges to create another spanning tree of the same graph.

If some of the edges of G have the same weight, then there are chances that more than one MST is possible for that graph.

If every edge has the same weight, then all the spanning trees of G are a minimum spanning tree.

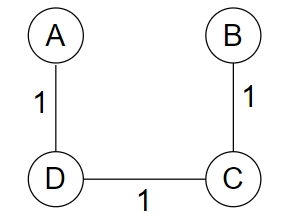
Example: 

All the possible spanning trees of Figure 1 are shown below.

As all the edges have the same weight, all the spanning trees are minimum spanning trees with a weight of 3.

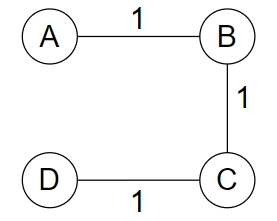
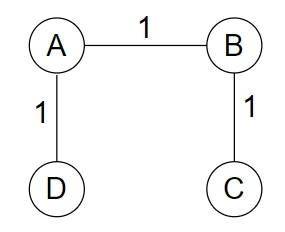
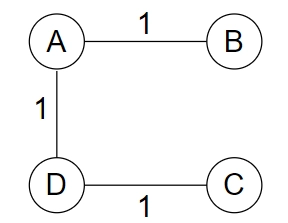
Uniqueness

Property: There will be only one, i.e., a unique minimal spanning tree if each edge has a distinct weight. 

In the example shown below, there is only one MST possible because each edge has a distinct weight.

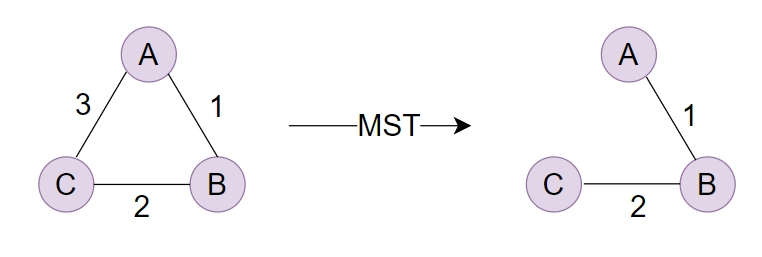
The Cut Property

Definition of a Cut: A cut can be described in graph theory as a partition that divides a graph into two distinct subsets.

In a connected graph G(V, E), a cut C = (S1, S2) divides the vertex set V into two disjoint subsets S1 and S2.

Cut Set: For a connected graph G(V, E), a cut set of a cut C(S1, S2) can be defined as the set of edges that have one endpoint in S1 and the other in S2.

The Cut Property: If the weight of an edge E in the cut-set of C is strictly less than the weights of all other edges in the cut-set of C, then this edge belongs to all the MSTs of the graph.

Example: Given below is a connected and undirected graph G.

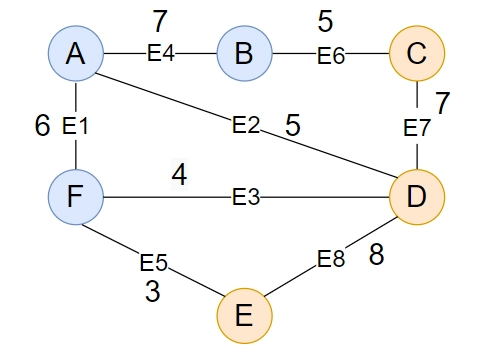
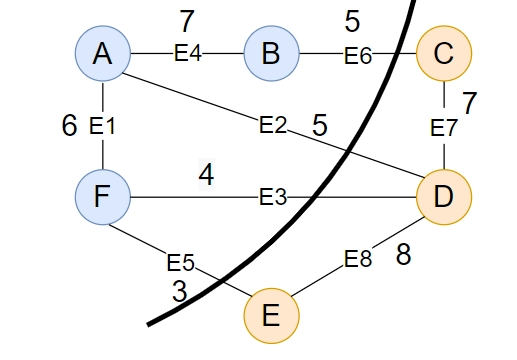
Cut C will divide the graph into two subgraphs S1 and S2. Blue vertices are the part of S1, and red vertices are the part of S2.

Cut set includes {E6, E2, E3, E5}.

Let’s draw the MST of the above graph.

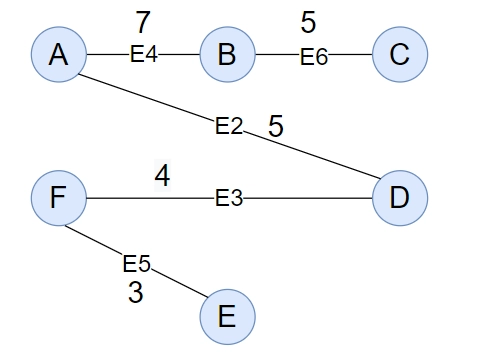
As you can see, this is one of G's minimum spanning trees, and the edge E5 is present. Hence, the cut property is working fine for G.

You can draw other possible MSTs of G and see that E5 is always there.

Click here to know more about the cut property and its proof.

Cycle Property

The Cycle property states that: If there is a cycle in the graph and if the weight of an edge E of a cycle C in the graph is greater than the individual weights of all other edges of C, then this edge cannot belong to an MST. 

For example, the graph shown in the cut property, E8 (in cycle FDE), will never be there in any of the MSTs of G.

Miscellaneous

1. Minimum cost Edge: If a graph's minimum cost edge is unique, it is included in all the MSTs.
2. The spanning-tree will become cyclic if a new edge is added because every spanning tree is minimally acyclic.
3. The spanning tree is minimally linked, which means that removing any edge from the spanning tree will disconnect the graph.

Check out this problem - No of Spanning Trees in a Graph