
Introduction
Propositional Logic transforms a complete sentence into a symbol. It makes it logical, whereas, in First-Order Logic, a particular sentence will be made that involves relations, functions, and constants. This article has popular propositional and first-order logic questions in past year gate exams.
Questions
1. Give the logical translation of the statement? [GATE CS 2013]
“None of my friends are perfect.”

Answer: D
Explanation:
F(x) ==> x is my friend
P(x) ==> x is perfect

2. Which of the following are NOT logically equivalent to ¬∃x( ∀y(α) ∧ ∀z(β))? [GATE CS 2013]

Answer: A, D
Explanation:
¬ ∃ x ( ∀y(α) ∧ ∀z(β)) [ Given ]
=> ∀ x (¬∀y(α) ∨ ¬∀z(β)) [¬(∀x P(x)) <=> ∃ x¬P(x) and ¬(A∧B) = (¬A∨¬B)]
=> ∀ x ( ∀y(α) -> ¬∀z(β)) [¬P ∨ Q <=> P -> Q]
=> ∀ x ( ∀y(α) -> ∃z(¬β)) [¬(∀x P(x)) <=> ∃ x¬P(x)]
Hence the given statement is logically equal to statement C.
Now, we can write this statement:
=> ∀ x ( ∀z(β) -> ∃y(¬α) ) [If P ->Q, then by Result of Contrapositive, ¬Q-> ¬P]
And this statement is the same as statement B.
So, we can deduce that the given statement is NOT logically equivalent to statements A and D.
3. What is the correct translation of the subsequent statement into mathematical logic? [GATE CS 2012]
“Some real numbers are rational.”

Answer: C
Explanation:

Answer C is correct.
4. Which of the options below is CORRECT given three positive integers, x, y, z, and a predicate? [GATE CS 2013]
F(x) = ¬(x=1)∧∀y(∃z(x=y*z)⇒(y=x)∨(y=1))
- F(x) being true means that x has precisely two factors other than one and x.
- F(x) is always true irrespective of the value of x.
- F(x) being true means x is a number other than 1.
- F(x) being true means x is a prime number.
Answer: D
Explanation: So we can evaluate the predicate as:
F(x) = (¬(x=1))∧(∀y(∃z(x=y*z) ⇒ ((y=1)∨(y=x))))
F(x) being true implies x ≠ 1, and for all y, if there exists a z such that the x = y*z, then y must be 1 (i.e., z=x) or y must be equal to x (i.e., z=1).
It means that x has only two factors first is 1, and the second is x itself. This predicate defines the prime number.
5. Suppose the predicate F(x, y, t) represents the statement that individual x can fool individual y at time t. Which one of the statements best expresses the meaning of the following formula? [GATE CS 2010]
∀x∃y∃t(¬F(x, y, t))

Answer: C
Explanation:
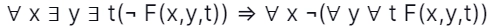
6. Which one below is the most appropriate logical formula to describe the following statement? [GATE CS 2009]
"Gold and silver ornaments are precious."
The notations used are: G(x): x is a gold ornament, S(x): x is a silver ornament, P(x): x is precious.
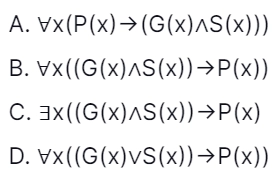
Answer: D
Explanation: This statement can be described as
=> For all x, x can be either silver or gold then the ornament x is precious
=> For all x, (G(x) v S(x))
=> P(X).
7. Let Graph(x) be a predicate that represents that x is a graph. Let Connected(x) be a predicate representing that x is connected. Which of the following first-order logic sentences DOES NOT mean the statement: “Not every graph is connected”? [GATE CS 2009]
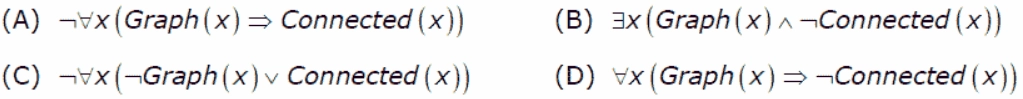
Answer: D
Explanation: Option A and option C are the same G(x)-->C(x) can also be written as ~G(x) or C(x), and they are the correct representation. Option C says: A graph is not connected, which is equivalent to the given sentence. Option D: Every x, the graph, is not connected. Option D is the correct choice.
8. Let FSA and PDA be the two predicates such that FSA(x) means x is a finite state automaton, and PDA(y) indicates that y is a pushdown automaton. Let the equivalent be another predicate such that equivalent(a, b) means a and b are equivalent. Which of the following first-order logic statements represents the following: Each finite state automaton has an equivalent pushdown automaton. [GATE CS 2008]
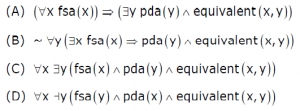
Answer: A
Explanation: Evaluating each option -
(A) If everything is an FSA, then an equivalent PDA exists for everything.
(B) It's not the case that for all y, if there exists an FSA, then it has an equivalent PDA.
(C) Everything is an FSA and has an equivalent PDA.
(D) Everything is a PDA and exists an equivalent FSA.
Hence, option (A) is correct.
9. What is the first-order predicate calculus statement equivalent to the following? Some students like every teacher: [GATE CS 2005]
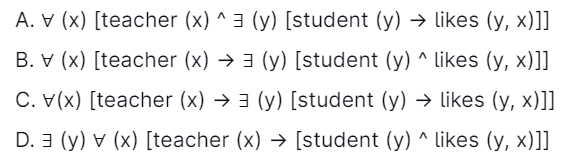
Answer: B
Explanation: If X is a teacher, then there exists some Y who is a student and likes X.
A. Statement: If X is a teacher, there is a Y. If Y is a student, Y likes X.
C. Statement: There exists a student who likes all the teachers.
D. Statement: Everyone is a teacher, and there is a Y. If Y is a student, then y likes X.
10. P and Q are the following two propositions. Which of the subsequent logical expressions are equivalent? [GATE CS 2008]
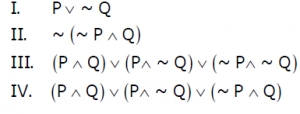

Answer: C
Explanation: I and II are the same by Demorgan's law
The IIIrd can be simplified to I.
= P∧(Q∨¬Q)∨(¬P∧¬Q)
= P∨(¬P∧¬Q)
= (P∨¬P)∧(P∨¬Q)
= (P∨¬Q)
11. Let Graph(x) be a predicate conveying that x is a graph. Let Connected(x) be a predicate which means that x is connected. Which of the subsequent first order logic sentences DOES NOT convey the statement: [GATE-CS-2007]
“Not every graph is connected”
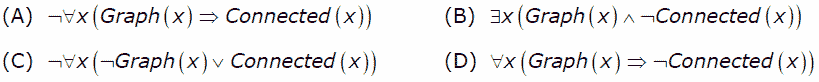
Answer: D
Explanation: Option A and option C are the same G(x)-->C(x) can also be written as ~G(x) or C(x), and they are the correct representation. Option C says: A graph is not connected, equivalent to the given sentence. Option D: Every x, a graph, is not connected. Hence, option D is the correct choice.
12. Which of the below is TRUE about formulae in Conjunctive Normal Form? [GATE-CS-2007]
A. There is a truth assignment for any formula for which at least half the clauses evaluate true.
B. There is a truth assignment for any formula for which all the clauses evaluate true.
C. There is a formula such that at most one-fourth of the clauses evaluate to true for each truth assignment.
D. None of the above.
Answer: A
Explanation: We can prove a truth assignment for which at least half the clauses evaluate true for any formula. Proof: Suppose an arbitrary truth assignment. For each of its clauses ‘j,’ introduce a random variable. Xj = 1 if clause ‘j’ is met Xj = 0 else Then, X = summation of (j * Xj) is the number of satisfied clauses. Given any clause ’c,’ it is unsatisfied only if all of its ‘k’ constituent literals evaluate to false as the OR operator joins them. Now, because each literal within a clause has a 1/2 chance of estimating true independently of any of the truth values of any of the other literals, the probability that they are false is (1 / 2)k. Hence, the probability that ‘c’ is satisfied = 1 − (1 / 2)k So, E(Xj) = 1 * (1 / 2)k = (1 / 2)k Therefore, E(Xj) >= 1/2 Summation on both sides to get E(X). Thus, we have E(X) = summation of (j * Xj) >= m/2 where ‘m’ is the number of clauses. E(X) represents the expected number of satisfied clauses. Thus, an assignment must exist that satisfies at least half of the clauses.
13. Which one of the following propositional logic formulas is TRUE when precisely two of p, q, and r are TRUE? [GATE-CS-2014-(Set-1)]
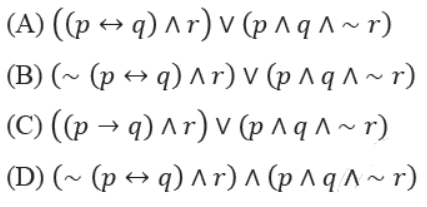
Answer: B
Explanation: The truth table of three variables and the output will be 1 (true) only when precisely two variables are 1 (true). Else outcome will be 0 (false). Therefore,
p q r Output (f)
----------------------------------
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
14. Which one of the subsequent Boolean expressions is NOT a tautology? [GATE-CS-2014-(Set-2)]
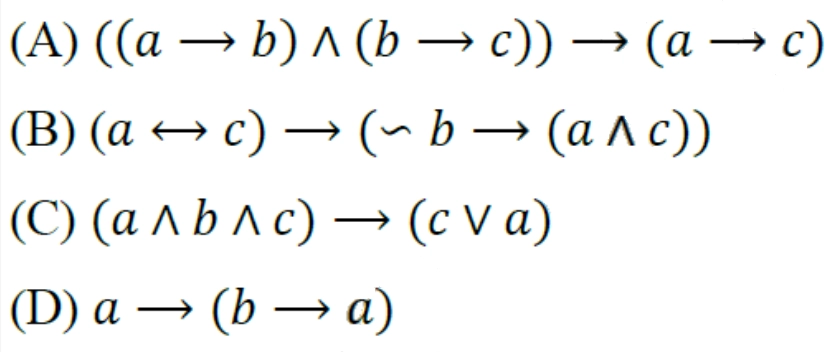
Answer: B
Explanation: (A) a -> b means if ‘a’ is true, then ‘b’ is also true.
Now, ‘b’ is true. Therefore, ‘c’ is also true.
=> Using transitivity rule , a -> c
(B) a <-> c is true if both ‘a’ and ‘c’ have identical values.
Let ‘a’, ‘b,’ and c’ be false.
Expression ‘a and b‘ is false, and expression ‘not b’ is true.
RHS of the given equation should be true. But it estimates to be false. Therefore, contradiction is there.
Hence, option (B) is not a tautology.
(C) Let ‘a’ and ‘c’ be false. ’b’ be true
a and b and c are false
c or a is false
(D) Let ‘b’ be true.
b -> a means if ‘b’ is true, then ‘a’ is also true.
Therefore, ‘a’ and ‘b’ are both true.
15. The CORRECT formula for the following sentence is? [GATE-CS-2014-(Set-3)]
“not all rainy days are cold”
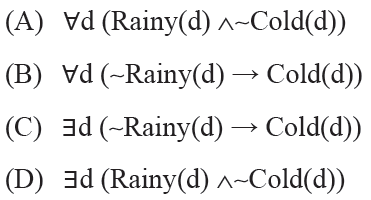
Answer: D
Explanation: (A) Note that (p ∧ ~q) ≡ ~(p -> q). So it means rainy day to cold implication is false for all days. It means non-rainy days are cold. (B) If the day is not rainy, it is cold all days. [Non-Rainy days are cold] (C) There exist some days for which not being rainy implies cold. [Some non-rainy days are cold] (D) Note that (p ∧ ~q) ≡ ~(p -> q). So it means rainy day to cold implication is false for some days. It means not all rainy days are cold.
16. Which one of the first-order predicate calculus statements below correctly expresses the following English statement? [GATE-CS-2006]


Answer: D
Explanation: This statement, "Tigers and lions attack if they are hungry or threatened," means that if an animal is either a tiger or a lion, it will attack if it is hungry or threatened. So option (D) is correct.
In the statement, don't get confused by "and" between tigers and lions. This "and" doesn't suggest that we will write "tiger(x) ∧ lion(x)" since that would have told that an animal is both tiger and lion, which is not what we want.
17. Consider the subsequent propositional statements: P1 : ((A ∧ B) → C)) ≡ ((A → C) ∧ (B → C)) P2 : ((A ∨ B) → C)) ≡ ((B → C) ∨ (A → C)) Which one of the following is true? [GATE-CS-2006]

Answer: D
Explanation: The easiest way to solve this question is by creating truth tables for the expressions given. Note that P1 will be a tautology if the truth table for the left term is the same as the truth table for the correct term. The same holds for P2 also.

18. A logical binary relation □ is defined as follows:
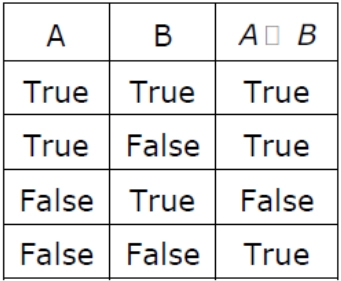
Let ~ be the unary negation (NOT) operator, with higher precedence than □.
Which one of the below is equivalent to A ∧ B? [GATE-CS-2006]
(A) (~A □ B)
(B) ~(A □ ~B)
(C) ~(~A □ ~B)
(D) ~(~A □ B)
Answer: D
Explanation: In A ∧ B, we have three entries False and one True. It is the opposite case in the table, so we have to negate A □ B. Moreover, we want True only when both A and B are true, so in the 3rd entry (which becomes true after negation), we want both true, so we have to negate A.
So A ∧ B ≡ ~(~A □ B), so option (D) is correct.
19. Let P, Q, and R be the three atomic prepositional assertions. Let X indicate (P v Q) → R and Y indicate (P → R) v (Q → R). Which of the following is a tautology? [GATE-CS-2005 ]
A. X ≡ Y
B. X → Y
C. Y → X
D. ¬ Y → X
Answer: B
Explanation: X = (P ⋁ Q) → R
= ~(P ⋁ Q) ⋁ R
= (~P ⋀ ~Q) ⋁ R
= (~P ⋁ R) ⋀ (~Q ⋁ R)
= (P → R) ⋀ (Q → R)
X → Y is true as (A ⋀ B) → (A ⋁ B) is always TRUE
but the reverse implication is not always true.
20. Determine the correct translation into the logical notation of the subsequent assertion. [GATE-CS-2004]
"Some boys in the class are taller than all the girls."
Note: taller(x,y) is true if x is taller than y.
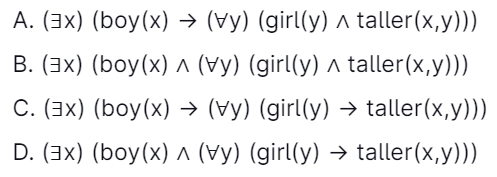
Answer: D
Explanation: Many people get confused about when ∧ and when to use →. This question tests precisely that. We use ∧ it when we want to say that both predicates in this statement are always true, no matter the value of x. We use → it when we desire to say that although there is no need for the left predicate always to be true, the right predicate must also be true whenever it becomes true. D means there exist some boys x which taller than all girls y.
21. The following propositional statement is [GATE-CS-2004]
(P → (Q v R)) → ((P ^ Q) → R)
A. a contradiction
B. valid
C. satisfiable but not valid
D. none of the above
Answer: C
Explanation: A formula is satisfactory if at least one assignment for which it is true. This formula is acceptable as there are seven assignments for which it is true. A formula is valid if it is true for all assignments, which is not the case here.
Hence, option (C) is correct.
22. Which of the below is a valid first order formula? (Here, α and β are first-order formulae with x as their only free variable) [GATE-CS-2003]
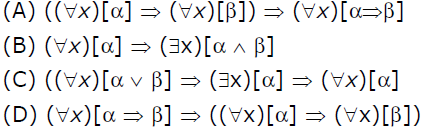
Answer: D
23. Consider the subsequent formula a and its two interpretations, I1 and I2. Which of the subsequent statements is true? [GATE-CS-2003]
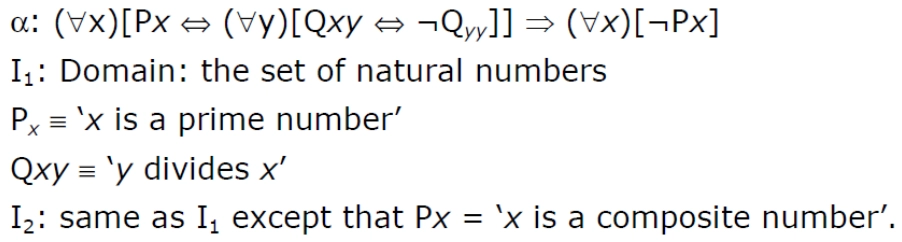
(A) I1 satisfies α, I2 does not
(B) I2 satisfies α, I1 does not
(C) Neither I2 nor I2 satisfies α
(D) Both I1 and I2 satisfy α
Answer: D
Explanation:
- First of all, note that, in α, ¬Qyy is always false because every number divides itself.
- Note that the rightmost formula (∀x)[¬Px] is always wrong because it is not the case that every number is not a prime number (in the case of I1), nor it is the case that each number is not a composite number (in case of I2).
- Note that variable x in this expression is not the same as variable x on the left side.
They are independent. We can rewrite α as α:(∀x)[Px⇔(∀y)[Qxy⇔¬Qyy]]⇒(∀z)[¬Pz].
Let us consider I1 first. So let us allocate some value to x and see if it satisfies α. We can partition assignments of x into three parts: when x is prime when x is composite when x is 1.
- When x is prime: Px is true; Qxy is false for all y except one because only 1 divides x. So formula Qxy⇔¬Qyy is true for all y except 1, but due to ∀y outside this, whole formula ∀y[Qxy⇔¬Qyy] becomes false because it would have been true if Qxy⇔¬Qyy was true for every y.
- So now [Px⇔(∀y)[Qxy⇔¬Qyy]] becomes false for all x whenever x is prime.
- Since for some x (x is prime), [Px⇔(∀y)[Qxy⇔¬Qyy]] is false, so (∀x)[Px⇔(∀y)[Qxy⇔¬Qyy]] is false, since false⇒ false is true, so α is true in I1, and we don't need other cases of x.
- Now consider I2. Here, we can argue in the same way as we did in cases of I1. Here the point of x being composite leads to false⇒false, so α is also true in I2; hence option (D) is correct.
24. Consider the following logic program P
A(x) <- B(x, y), C(y) <- B(x,x)
Which of the below first-order sentences is equivalent to P? [GATE-CS-2003]
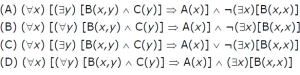
Answer: C
25. The following resolution rule is used in logic programming.
Derive clause (P ∨ Q) from clauses (P ∨ R), (Q ∨ ¬R)
Which of the following statements related to this rule is FALSE? [GATE-CS-2003]
A. ((P ∨ R) ∧ (Q ∨ ¬R)) ⇒ (P ∨ Q) is logically valid.
B. (P ∨ Q) ⇒ ((P ∨ R)) ∧ (Q ∨ ¬R)) is logically valid.
C. (P ∨ Q) is satisfiable if and only if (P ∨ R) ∨ (Q ∨ ¬R) is satisfiable.
D. (P ∨ Q) ⇒ FALSE if and only if both P and Q are unsatisfiable.
Answer: A
Explanation: Option (A) itself is the definition of resolution.
26. "If X, then Y unless Z" is represented by which of the following formulae in propositional logic? ("¬" is negation, "^" is a conjunction, and "→" is the implication) [GATE-CS-2002]
A. (X ^ ¬ Z) → Y
B. (X ^ Y) → ¬ Z
C. (X → (Y ^ ¬ Z)
D. (X → Y(^ ¬ Z)
Answer: A
Explanation: "If X then Y unless Z" denotes, if Z doesn't occur, X indicates Y, i.e., ¬Z→(X→Y), which is equal to Z ∨ (X→Y) (since P→Q ≡ ¬P ∨ Q), which is then equal to Z ∨ (¬X ∨ Y). Now, look into options which one matches this. Hence, option A is (X∧¬Z)→Y = ¬( (X∧¬Z) ) ∨ Y = (¬X∨Z) ∨ Y, which matches our expression. Thus, option (A) is correct.
27. Consider two well-formed formulas in propositional logic. [GATE-CS-2001]
F1: P ⇒ ¬P
F2: (P⇒¬P) ∨ (¬P⇒P)
Which of the subsequent statements is correct?
A. F1 and F2 are both satisfactory.
B. F1 is unsatisfiable, F2 is satisfiable.
C. F1 is unsatisfiable, and F2 is valid.
D. F1 is satisfactory, and F2 is valid.
Answer: D
Explanation: The concept behind this solution is:
a) Satisfiable
If there is an assignment of truth values, that expression is accurate.
b) Unsatisfiable
If there is no such assignment that makes the expression true
c) Valid
If the expression is Tautology
Here, P => Q is nothing but –P v Q
F1: P => -P = -P v –P = -P
F1 will be true if P is false, and F1 will be false when P is true, so F1 is Satisfiable.
F2: (P => -P) v (-P => P) which is equals to (-P v-P) v (-(-P) v P) = (-P) v (P) = Tautology
So, F1 is Satisfiable, and F2 is valid.
28. Let a, b, c, d be the propositions. Assume that a ↔ (b V-b) and b ↔ c hold the equivalences. Then the truth value of the formula (a ∧ b) → (a ∧ c) ∨ d) is always: [GATE-CS-2000]
A. False
B. True
C. Same as the truth value of d
D. Same as the truth value of b
Answer: B
Explanation: Notations (identities):
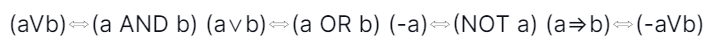
29. Which one of the below is not equivalent to p←→q? [GATE-CS-2015 (Set 1)]
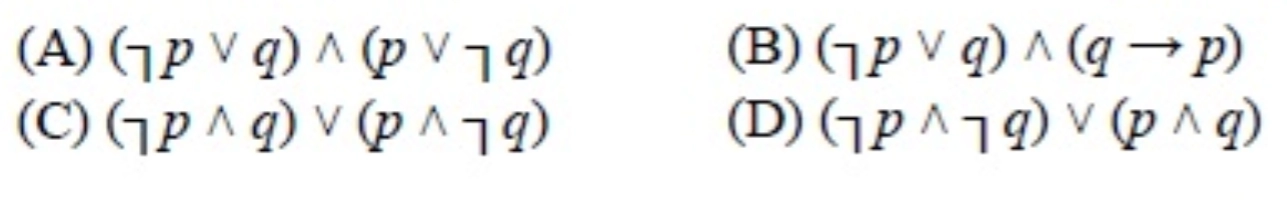
Answer: C
Explanation: This question is the revision of the basics of propositional logic. The conjunction of p and q, represented by p∧q, is the proposition ‘p and q’. The p ∧ q is true when both p and q are True. The disjunction of p and q, represented by p∨q, is the proposition ‘p or q’. The p∨q is False when both p and q are False. Logical Implication is a type of association between two sentences or statements. Implied by ‘p → q’. The p → q conditional statement is false when p is true & q is false, and true otherwise. i.e., p → q = ¬p ∨ q is Bicondition. A biconditional statement is a compound statement created by merging two conditionals under “and.” Biconditionals are true when both statements have the same truth value.
Solution: p↔q means both p→q and q→p p→q are equal to ⌉p ∨ q, and q is equal to ⌉q ∨ p. So A and B are fine. D is a distinct way of writing A p ↔ q = (p→ q) ∧ (q→p) = (⌉p ∨ q) ∧ (q → p). Option (D) is (⌉p ∧ ⌉q) ∨ (p ∧ q), which is the only option that is not equivalent to p↔q is an option (C). Hence, option (C) is correct.
30. Consider the subsequent two statements.

Which one of the subsequent statements follows from S1 and S2 as per the sound inference rules of logic? [GATE-CS-2015 (Set 2)]

Answer: C
Explanation: S1: If a nominee is known to be corrupt, then he will not be elected.
S2: If a nominee is kind, he will be selected.
If p → q, then ¬q → ¬p
So from S1, elected → not corrupt
and S2 is kind → elected,
Therefore, kind, → not corrupt




